贵州省兴义市第五中学 562400
摘要:在新课改的不断推进发展下,传统单一的灌输式填鸭式教学已经不能满足学生的需求。为此我们必须将教学策略不断地进行优化完善,需要有效地去结合数学思想方式以及解题方式。因为我国教育属于应试教育,所以不管是老师还是学生在学习过程中只注重成绩,所以,在教学过程中让学生们大量做题本不能从根本上提高学生的解题能力,这一现象的发生会对学生今后的发展产生不利影响。要想提高学生数学素养,务必要提高学生的解题能力,对学生今后的发展也意想不到的好处。因此加强培养高中学生的解题能力是我国高中数学老师的根本任务。鉴于此,本文对高中数学解三角形中求最值的方法进行了探索。
关键词:高中数学;解三角形;求最值;方法探索
随着新课改革进程的不断推进,传统的教学方式已经不能满足学生和社会的需求,因此,教师要及时改变教学策略。由于学生长时间受到应试教育的影响,大部分教师之注重学生学习成绩的培养,让学生做大量的题,而忽视了学生解题能力的培养,这样的教学状态下,对学生的发展很不利。学生的解题能力直接影响到学生的数学思维,学生思维能力的发展也对日后有着很大的影响,因此教师对学生的解题能力加以重视。
一、高中阶段进行数学解题能力培养的重要性
在高中阶段,在接受数学教学引导的过程中,学生本身已经形成了一定的认知能力,如果教师不注重教学方法,而只是被动且生硬地向学生灌输知识就很难收到理想的教学效果,反而容易导致学生形成逆反心理。因此,教师在高中数学教学过程中,要能够顺应学生的思维认知习惯,使他们在数学学习的过程中获得乐趣及成就感。比如,对于一些数学基础较差的学生来说,他们学习高中数学的难度往往比较大,也很吃力。在教育改革推进的过程中,教师要认识到,对于高中数学教学来说,不应仅仅将成绩作为开展教学以及评判的唯一标准,最为主要的是要让学生掌握数学学习的方法,并考察学生的综合能力,通过帮助学生掌握数学学习的规律,提高学习效率,从而将教学的重点放在能力提升上。
对于高中阶段的学生来说,掌握正确的解题方法也是开展数学学习的关键之一,只有不断提升自己的数学解题能力,发现琐碎的知识点之间的联系,才能够掌握数学学习的秘诀,并且举一反三,将在数学课上形成的知识和经验嫁接到日常生活中。由此,才能实现课本知识和日常生活的融会贯通,并理解数学知识,掌握问题解决的规律,这也正是高中阶段实现数学解题能力培养的重中之重。
高中数学解三角形求最值解题方法
在三角形中,求某些不确定量(式)的取值范围或最值,是高考中常见题型,归纳起来主要体现在:求角、边、周长、面积的范围或最值.这类题型知识能力的要求高、难度大,不仅要求学生要具备灵活运用正(余)弦定理的准确计算能力,而且更要求学生要有较强的观察、理解、分析与推理的思维演变能力.因此要解决此类问题,首先要充分掌握三角形中所存在的等量关系,比如,A+B+C=π,a=2RsinA,b = 2RsinB, c = 2RsinC(其中R为三角形的外接圆半径),c2=a2+b2-2abcosC,以及一些不等关系,比如,|a-b| ,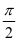 < A + B <π,a2+b2>c2等;同时结合题设条件把所求问题进行合情推理、恒等变换(边化角,角化边),并从中寻找出引起不定量变化的参变量,再充分利用不等式相关性质、三角函数的有界性等,求出相关不定量(式)的最值或取值范围,进而厘清问题的本质。
< A + B <π,a2+b2>c2等;同时结合题设条件把所求问题进行合情推理、恒等变换(边化角,角化边),并从中寻找出引起不定量变化的参变量,再充分利用不等式相关性质、三角函数的有界性等,求出相关不定量(式)的最值或取值范围,进而厘清问题的本质。
1、角的范围或最值
“角”是研究三角函数的核心,三角函数的取值范围与角的大小紧密关联,所以研究三角形中的“角”的取值范围或最值可借助三角函数的有界性,或利用正(余)弦定理把三角转换成边、再结合不等式的相关性质进行求解。
例1,在△ABC中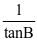 +
+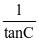 =
=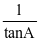 ,则cosA的取值范围为( )
,则cosA的取值范围为( )
A.(0,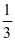 ) B.[
) B.[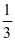 ,1) C.(0,
,1) C.(0,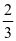 ) D.[
) D.[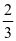 ,1)
,1)
分析,根据已知条件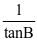 +
+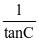 =
=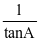 及正弦定理得:cosA=
及正弦定理得:cosA=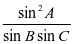 =
=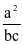 ,而由余弦定理知:cosA=
,而由余弦定理知:cosA=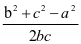 ,所以
,所以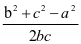 =
=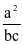 ,因此,得到三角形的三边关系:3a2=b2+c2,进而可得:cosA=
,因此,得到三角形的三边关系:3a2=b2+c2,进而可得:cosA=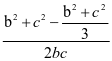 =
=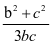 ,结合均值不等式知:cosA=
,结合均值不等式知:cosA=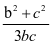 ≥
≥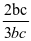 =
=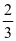 ,当且仅当b=c时取等号,所以cosA的取值范围为[
,当且仅当b=c时取等号,所以cosA的取值范围为[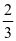 ,1)。
,1)。
2、边的范围或最值
正(余)弦定理告诉了三角形中边与角相互转换的规律,这就凸显了正(余)弦定理的木质所在,因此研究和探讨边的取值范围或最值时,充分抓住边与角两元素的各自的特点,利用正(余)弦定理进行合理转换,问题就可以迎刃而解.
例2,已知△ABC的内角A,B,C的对边分别为a,b,c,且满足(a2+b2-c2)(acosB+bcosA)=abc,若a+b=2,则c的取值范围是 。
分析,该题条件是边与角混合关系式,从结构上看,先用余弦定理进行恒等变换,可得等式为2cosC(acosB+bcosA)=c,再利用正弦定理得cosC=
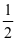 ,即C=
,即C=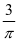 ,所以由余弦定理得c2=a2+b2-2abcosC=(a+b)2-3ab,结合题设条件a+b=2和均值不等式可得ab ≤1,当且仅当a=b=1时等号成立,所以c2≥1,即c≥1,又由三角形ABC中的不等关系知:c
,所以由余弦定理得c2=a2+b2-2abcosC=(a+b)2-3ab,结合题设条件a+b=2和均值不等式可得ab ≤1,当且仅当a=b=1时等号成立,所以c2≥1,即c≥1,又由三角形ABC中的不等关系知:c
例3,△ABC中角A,B,C所对的边分别为a,b,c,且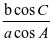 +
+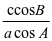 =2
=2
分析,(1)由题设条件中的等式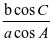 +
+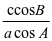 =2可得A=60°;(2)根据题意,欲求△ABC周长的最大值,即求b+c的最大值,由题设条件可得△ABC的外接圆
=2可得A=60°;(2)根据题意,欲求△ABC周长的最大值,即求b+c的最大值,由题设条件可得△ABC的外接圆
直径为2R=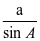 =
=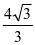 ,所以可把边b,c分别转化为b=
,所以可把边b,c分别转化为b=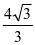 sinB,c=
sinB,c=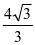 sinC,从而化简整理可得:
sinC,从而化简整理可得:
B+c=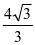 (sinB+sinC)=4(
(sinB+sinC)=4(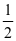 cosC+
cosC+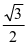 sinC)=4sin(C+
sinC)=4sin(C+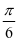 )。
)。
所以三角形ABC的周长l=2+4sin(C+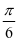 ),由于0 <
),由于0 <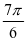 ,再结合三角函数的有界性可知,当C=
,再结合三角函数的有界性可知,当C=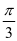 时,△ABC的周长的最大值为6。
时,△ABC的周长的最大值为6。
[1]王娓娓,任秀丽.赏析解三角形中的最值问题[J].高中数理化,2018,(17):19-20.
[2]张凯华.一道三角形面积最值题的多解剖析[J].中学数学,2018,(19):74-75.