思而教，教而思——让反思伴随数学教学的始终

思而教，教而思——让反思伴随数学教学的始终

宋亚娟

江苏省张家港市南丰中学

笔者在苏科版初中数学九年级上册第2章圆的第一课时《圆》的这节内容的教学时，设置了一个思考题“已知一个点到圆上的点的最大距离是5，最小距离是1，则这个圆的半径是 ．”这是基于学生在本节课上刚学习了点与圆的位置关系，利用点与圆的位置关系来分析思考，首先这个点的位置在哪里？圆上，圆内，圆外，再结合题目含义排除点在圆上这种情况，从而展开“点在圆内，点在圆外”分类讨论。那么如何作出最大距离和最小距离的线段，怎么引导学生思考点到圆上的点的最大距离和最小距离呢？这是解决本题的一个难点。

其实圆上有无数个点，如果考虑圆内的点与圆上的点的距离，无非是连接这点与圆上任意一点，这两点之间的距离即为所分析的距离。何时会呈现所连接的两点线段最长或最短，这个过程可以让学生自己去操作思考，基于这个过程之后，肯定有学生会发现一种特殊的情况：即当圆内这一点与圆上一点连接的线段所在直线经过圆心时，可能就会出现最大距离和最小距离。那么为什么这个就是所谓的最大距离和最小距离呢？下面笔者做了一个分析：

如图1所示：当点P在圆O内时，线段PF的长度是点P到圆O上的点的最大距离，为什么？线段PE的长度是点P到圆O上的点的最小距离，为什么？

证明：在圆O上任取一点D，连接OD，在△OPD中，OD+OP＞PD,又因为OD=OF，即OF+OP＞PD，则有PF＞PD，所以线段PF的长度是点P到圆O上的点的最大距离；

在△OPD中，OD－OP＜PD ，又因为OD=OE，即OE－OP＜PD，则有PE＜PD，所以线段PE的长度是点P到圆O上的点的最小距离。

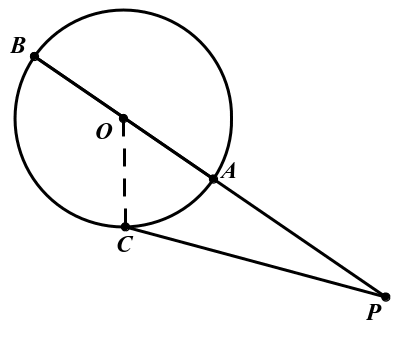
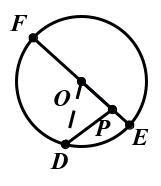
图1 图2

如图2所示：当点P在圆O外时，线段PB的长度是点P到圆O上的点的最大距离，为什么？线段PA的长度是点P到圆O上的点的最小距离，为什么？

证明：在圆O上任取一点C，连接OC，在△OPC中，OC+OP＞PC,又因为OC=OB，即OB+OP＞PC，则有PB＞PC，所以线段PB的长度是点P到圆O上的点的最大距离；

在△OPD中，OP－OC＜PC ，又因为OC=OA，即OP－OA＜PC，则有PA＜PC，所以线段PA的长度是点P到圆O上的点的最小距离。

笔者就本题教学的一点反思：1.点与圆上各点之间的距离，学生是否会联想到点与直线上各点之间的距离，即有直线型图形中的垂线段最短，即点与垂足的距离最短。让学生体验圆与直线型图形的联系， 那么是否可以这样思考：点与圆上各点之间的距离是不是也可以作垂直，而圆是一条封闭的曲线，不可以作垂直，是否可以尝试作点与圆心所在直径的垂线，这样就产生了后面学习的圆的切线问题，即点与两个切点之间的距离，一个是最大距离，一个是最小距离。

其实学生在平时的解题中，可能更在乎求出答案，而没有追究为什么会这么求，最终的结果就是碰到题目不会思考，不知道该从哪个方面着手，更不知道该用什么方法解决，即不能“对症下药”。有时我们教师在教学的时候也会存在这样的情况，往往只会教学生应该这样去解决问题，而没有从源头分析为什么要这样去做。特别在新授课的时候，定理的由来比运用定理解决问题更为重要。

笔者在《圆的对称性——垂径定理》的教学时，对于垂径定理的证明进行了如下的过程；

先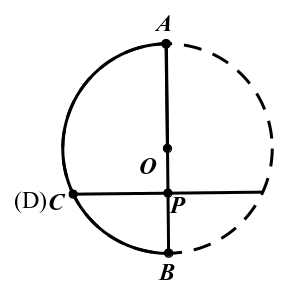 运用图形运动的方法(叠合法)证明，将图3中的弧ADB沿着直径AB翻折，因为圆是轴对称图形，过圆心的任意一条直线都是它的对称轴，所以弧ADB与弧ACB 重合。又因为∠APD=∠APC=90°，所以射线PD与射线PC重合，于是点D与点C重合。即PC=PD，弧AC=弧AD，弧BC=弧BD。

图3 图4

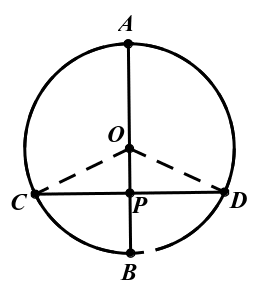
再运用“三段论证”加以证明；如图4，AB是圆O的直径，CD是圆O的弦，AB⊥CD，垂足为P。连接OC，OD，在△OCD中，因为OC=OD，OP⊥CD，所以PC=PD，∠BOC=∠BOD，所以∠AOC=∠AOD，所以弧AC=弧AD，弧BC=弧BD。

笔者就定理证明教学的一点反思：在这个定理的证明过程的教学中，前者是在操作中让学生感受证实垂径定理的实质是根据圆的轴对称性得来的。后者是运用直线型图形等腰三角形的“三线合一”的性质得到OP既是中线又是角平分线，从而得到弧的相等。既有合情推理，符合学生的认知规律，又有演绎推理，规范学生的书写，理清来龙去脉。很多时候学生随着所学知识的越多，越容易忘记定理的内容，但他还是会记住本源的方法。或者从另一方面来说随着经历的证明过程越是细致，方法越多样，学生的感悟也就越多，印象也就越深刻，学习数学的兴趣也就越高。从而达到主动学习，主动研究。