辽宁科技学院 (辽宁 本溪 117022)
摘 要;生态系统模型模型多种多样,分析复杂,而且结论众多。本文运用高等数学理论和极限环定义来证明一类系统的极限环的唯一性,使生态系统模型模型的基础更加简洁。
关键词:生态系统模型 极限环 稳定点
在捕食者与食饵种群相互作用提出系统模型
![]()
![]() (1)
(1)
其中参数a,b,c1,c2,d,F![]() 均为常数。
均为常数。
x,y分别为表示食饵种群与捕食种群的密度。F为食饵种群的存放率。P(x.y)与q(x)均定义在区域R=![]()
水平等倾线q(x.y)=0 即![]()
铅直倾斜线p(x.y)=0 即y=![]() 有两个极值点。
有两个极值点。
![]()
![]()
当 F=0时,x1=0 x2=![]()
系统(1)有两个平衡点:
(![]() )与(
)与(![]() ) 其中
) 其中![]() ,
,![]()
![]() 设
设 ![]()
定
 理1 当
理1 当![]()
![]()
![]() 时,系统(1)在平衡点(x0,y0)外围至少存在一个极限环。 Y C B(x0,ky0)
时,系统(1)在平衡点(x0,y0)外围至少存在一个极限环。 Y C B(x0,ky0)
证


 :x=0为切直线
:x=0为切直线
又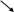
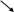


 y=0为轨线
y=0为轨线
(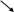
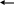






 x1,0)为平衡点 (x0,y0)
x1,0)为平衡点 (x0,y0)
做 水平直线CB
水平直线CB
y =ky0(k>1) O x0 A(x1,0) X
=ky0(k>1) O x0 A(x1,0) X ![]()
系统(1)的轨线从CB的上侧穿进入下侧。其次过点A(x1,0)和B(x0,ky0)做抛物线。弧AB![]()
令![]() 其中
其中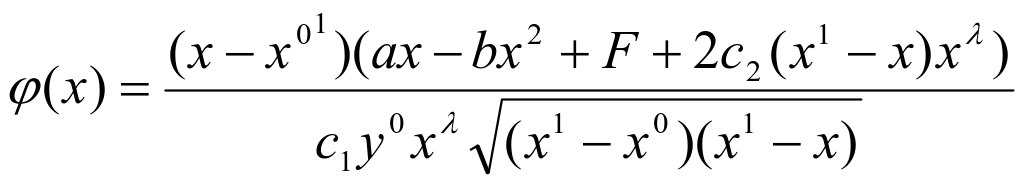
=![]() ,(其中
,(其中![]() )
)
显然![]() 在(x0.x1) 上连续。必有Max
在(x0.x1) 上连续。必有Max![]() 存在。
存在。
只须适当选取k> Max![]() 必有
必有![]() 成立。
成立。
从而系统(1)的轨线穿过它的方向如图所示。
于是闭合曲线L=0 ,ABCO与稳定点(x0.y0)构成环型域。
从而知系统(1)在(x0,y0)外围至少存在一个稳定的极限环。
定理2如果x102,那么系统(2)在区域R上存在的唯一的
稳定的极限环 。
证:令![]() 则系统(1)化为:
则系统(1)化为:
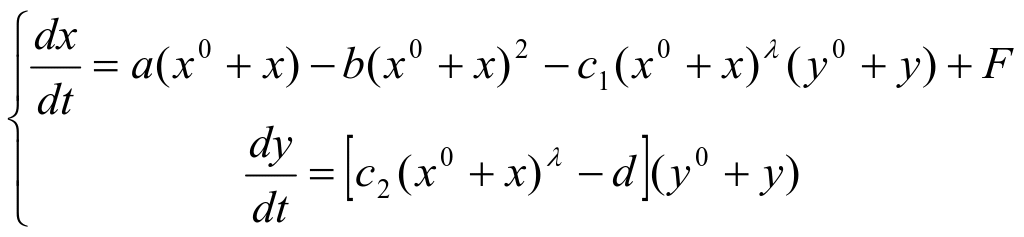 (2)
(2)
又令![]()
![]() 新变量
新变量![]() 仍用x,y,t表示,则(2)变为
仍用x,y,t表示,则(2)变为
![]() (3)
(3)
其中![]()
![]()
又![]()
![]()
![]() ,
, ![]()
由于x=x‘ x’=x+x0
于是 ![]()
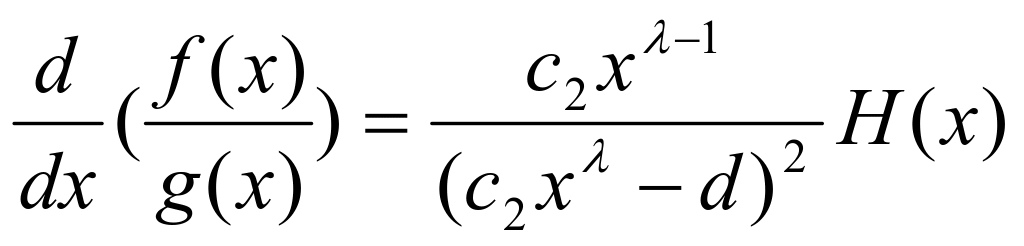
![]() 故在区域
故在区域![]() 上,
上,![]() 有唯一的驻点x=x0且又有
有唯一的驻点x=x0且又有![]()
故![]() 为极小值,即为最小值。所以有
为极小值,即为最小值。所以有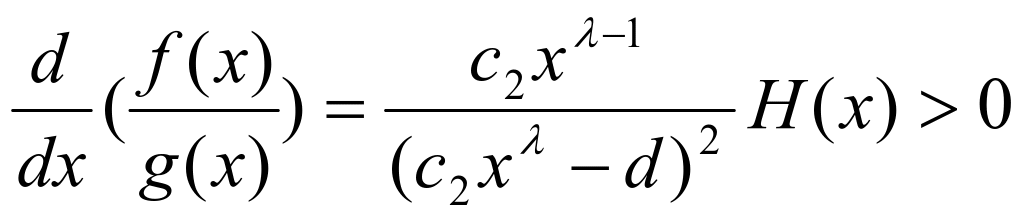
(![]() )成立
)成立
因此(3)满足![]() 中的唯一性定理的条件,从而最多只有一个极限环。所以在区域R上存在唯一一个极限环。
中的唯一性定理的条件,从而最多只有一个极限环。所以在区域R上存在唯一一个极限环。
参考文献:
[1] 蔡燧林 常微分方程定性理论引论 北京 高等教育出版社 1994
[2] 符天武 具有密度制约的一类微分生态系统的定性分析 湖南湖南科技出版社 1989
[3] 张芷芬 微分方程定性理论 北京 科技出版社 1995
[4] 李小燕 一类非线形系统的极限环 长沙电力学院学报 (自然科学版) 1996 NO 2
[5] 余昭旭 孔继涛 叶卓映 一类具有稀疏生态系统极限环《生物学学报》2001 ,04
[6] 刘娟 李医民具有收获效率生态系统极限环 《广东石油化工学院学报》2011,03
[7] 蒋武军一类分数阶捕食者—食饵模型 《甘肃高师学报》 2019, 05