中铁二局第六工程有限公司 ( 四川 成都 610000 )
提要:总结了线路正反算的常用积分计算方法,针对计算速度较快、计算精度较高的变步长辛普森积分算法在线路正反算中的弊端进行了研究,并提出解决办法。
关键词:线路正反算 变步长辛普森数值积分
1 引言
由于GPS-RTK、全站仪以及手簿等智能型计算设备在工程中的大规模应用,线路计算的统一模型研究也得到了较大的发展。李全信在《Gauss - Legendre 公式在线路坐标计算中的应用研究》一文中提出了高斯-勒让德五节点算法,娄平等在《利用缓和曲线的曲率确定其方程式的通用方法》中提出了高项展开公式,冯晓等在《不同类型缓和曲线的正算与反算的通用算法》中提出了复化辛普森算法等。对于上述各种算法在计算精度上和效率上都有不同程度提高,高斯-勒让德五节点算法由于不需要迭代计算而在计算效率上占优,在工程测量计算器中被广泛采用,但因其截断误差使计算精度上损失较大,不能在偏角极大的曲线计算中使用;其余数字积分算法计算精度较高,但因需迭代计算在计算效率上较高斯-勒让德五节点法等类似积分算法低,这些算法中,变步长辛普森积分算法在计算效率上相对较高,最为适宜。
2 缓和曲线通用计算积分公式
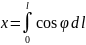 (1)
(1)
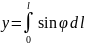 (2)
(2)
我国铁路、公路工程缓和曲线常采用三次抛物线
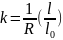 (3)
(3)
根据上式,可将直线、圆曲线、缓和曲线统一为如下积分公式:
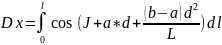 (4)
(4)
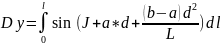 (5)
(5)
式中,J-曲线起始方位角;
a、b-曲线起始点曲率,直线为0,圆曲线为1/R,缓和曲线为1/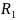 、1/
、1/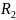 ;
;
d-计算长度
L-线元长度。
Dx,Dy-相对于起算点的坐标增量
3 变步长辛普森积分算法
对于定积分:
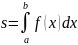 (6)
(6)
用梯形公式计算
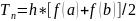 (7)
(7)
其中n=1,h=b-a且令Sn=Tn。
用变步长梯形法则计算
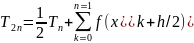 (8)
(8)
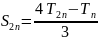 (9)
(9)
迭代计算,直到满足精度要求:
若Abs(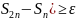 ,则令
,则令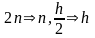 转到步骤(2)继续计算;否则结束,S2n即为所求的积分近似值。其中ε事先给定的求积精度。
转到步骤(2)继续计算;否则结束,S2n即为所求的积分近似值。其中ε事先给定的求积精度。
4 将变步长辛普森算法用vb.net代码实现
While e > ε‘ε为设置的需要的计算精度
Dim p As Double = 0
For i = 0 To n - 1
x1 = (i + 0.5) * h
Dim huai As Double = j + a * x1 + (b - a) * x1 ^ 2 / (2 * L)
x1 = Cos(huai)
p = p + x1
w = w + 1
Next
Dim u As Double = (t + h * p) / 2
v = (4 * u - t) / 3
e = Abs(v - s)
t = u : s = v
n = n + n : h = h / 2
End While
5 算法存在的整圆周期异常收敛的弊端
在对算法进行极端条件下测试中发现,当计算点位于线元终点且为整圆周期(偏角为360°或为其整倍数)时,结果是错误的,如对下表线元进行测试计算:
表一
线元序号 | 起点里程 | 起点x | 起点y | 线元长度 | R1 | R2 | 偏向 |
1 | 0+000 | 0 | 0 | 1256.63704 | ∞ | 200 | 右偏 |
2 | 0+000 | 0 | 0 | 2513.27408 | ∞ | 200 | 右偏 |
按照变步长辛普森算法计算线元终点的结果:
表二
线元序号 | 计算里程 | x | y | |
1 | 1+256.63704 | 1251.7499 | 82.4536 | |
2 | 2+513.27408 | 2361.0497 | 632.5901 | |
分析算法也可以看出,当曲线计算点位于整圆时,算法异常收敛,得到的结果是错误的,其根本原因在于三角函数的周期性。虽然在实际工程中,偏角为360°时极为少见,对于工程测量,仍然需要在算法上进行防范,以免在特殊情况下得到错误的结果,带来不必要的损失。
6 针对异常收敛的改进
从式(3)来看,以三次抛物线为模型的缓和曲线可以对曲线进行分解。结合目前线路反算采用切线迭代算法亦会出现异常收敛的不确定结果,为更好使用对半查找算法进行线路反算,将曲线分解的临界点设在180°处,当曲线偏角不超过180°时则不分解,超过180°时则按180°进行分解,从而避免计算点位于360°整圆处。表一测试线路按照改进算法后的正确结果为:
表三
线元序号 | 计算里程 | x | y | 备注 |
1 | 1+256.63704 | 469.9607 | 634.4190 | |
2 | 2+513.27408 | 613.5573 | 431.5489 | |
7 结束语
现阶段我国的基建设施迅猛发展,设计理念不断更新,追求线型而不过多的考虑经济因素,缓和曲线设计可能不再局限于常规设计,如连续盘旋的高原铁路、公路等,缓和曲线的偏角超过360°亦成为可能。本文在分析了各种数值积分方法的计算精度和计算效率上,针对计算精度可靠以及计算效率较高的变步长辛普森数值积分算法,提出了改进措施,并有利于解决线路反算使用切线迭代法异常收敛的弊端,从而彻底解决使用数值积分算法进行线路正反算存在的问题,通过实际应用,满足施工生产要求,具有较高的应用前景。
参考文献:
1、《Gauss - Legendre 公式在线路坐标计算中的应用研究》,李全信,《测绘通报》2008.6
2、《数值积分法计算线路中线坐标》,李孟山等,《石家庄铁道学院学报》1999.9
3、《不同缓和曲线正算和反算的通用算法》,冯晓等,《测绘通报》2008.6
4、《现代公路测量实用程序及其应用》,人民交通出版社,2005
5、《复杂地区道路的测设方法》,薛丽娟,《山西建筑》,2006
6、《数值分析》,李庆杨等,华中理工大学出版社,1988
7、《铁道工程测量学》,朱成磷等,中国铁道出版社,1989