江苏省淮安市金湖中学 邮政编码: 211600
我们先来应用正切相关的知识来解决这道题目:
在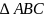 中,
中,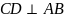 于D,且BD=3AD
于D,且BD=3AD
若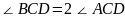 ,求
,求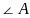 大小;
大小;
若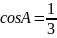 ,求
,求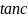 的值。
的值。
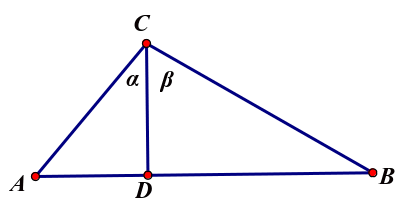
解:
设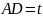 ,则
,则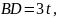 设
设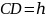
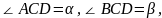
1.在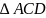 中,
中,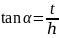 ,在
,在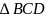 中,
中,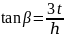 ,
,
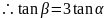
又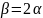 ,
,
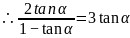
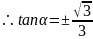 ,(负的的舍去)
,(负的的舍去)
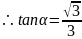
2.由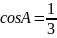 ,得:
,得: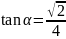 ,
,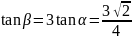 ,
,
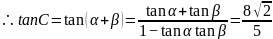 ,
,
我们下面来分析一下这道题:这道题的本质其实就是CD起到了决定性的作用,CD既起到了分割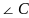 的作用,又起到了分割线段AB的作用,并且这道题目还给予了
的作用,又起到了分割线段AB的作用,并且这道题目还给予了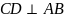 这个条件,也就给了我们使用正切的条件,但是我们其实在很多情况下,使用正弦余弦会比较多,垂直的条件往往在高中不会轻易给予,那么我们下面就围绕CD的长度以及CD分割的角和线段的关系进行讨论,可以预想的是如果把分割的角的相关参数设为自变量,把分割的线段的相关参数设为因变量,那么二者之间一定是存在着函数关系,易知这种关系绝对不是简单的线性关系,而且我们在探讨这种关系时可以通过所分割的角之间的关系和所分割的线段之间的关系来表达。
这个条件,也就给了我们使用正切的条件,但是我们其实在很多情况下,使用正弦余弦会比较多,垂直的条件往往在高中不会轻易给予,那么我们下面就围绕CD的长度以及CD分割的角和线段的关系进行讨论,可以预想的是如果把分割的角的相关参数设为自变量,把分割的线段的相关参数设为因变量,那么二者之间一定是存在着函数关系,易知这种关系绝对不是简单的线性关系,而且我们在探讨这种关系时可以通过所分割的角之间的关系和所分割的线段之间的关系来表达。
下面我们先讨论一次分割的情形:
如图:
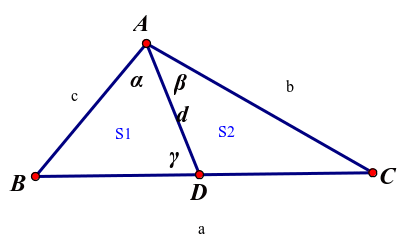
我们先来证明张角定理;
在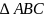 中给定
中给定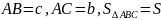 ,设
,设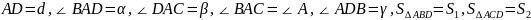 ,
,
知:
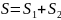 且
且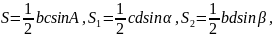
则: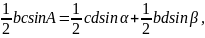
化简得: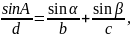
那么便可求得AD长: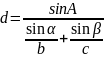 ,
,
下面探讨分割的“关系”:
“算两次”:在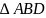 和
和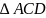 中关于γ分别使用一次正弦定理得:(当然也可以利用
中关于γ分别使用一次正弦定理得:(当然也可以利用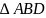 与
与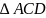 等高,底边比就等于面积比)
等高,底边比就等于面积比)
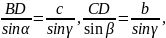
两式相除得: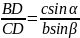
特殊情况:当c=b,α=β时,CD既平分BC,又平分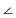 A
A
我们在分割一次的情况下,以及上述所给条件,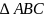 已经确定,我们设置高中知识相关和几个利用张角定理能够较为简单的处理的题目:
已经确定,我们设置高中知识相关和几个利用张角定理能够较为简单的处理的题目:
求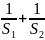 ,
,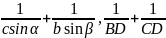 的最小值
的最小值
求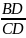 (适当条件下)
(适当条件下)
求DA+DC的最值
求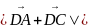 的最值
的最值
5.求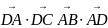 (适当条件下)
(适当条件下)
(只是简单的列举了一些题目,当然更多的需要读者自己开发、发现)
这里我们分享一种想法:上述题目其实就是两个大类,也是高中经常遇见的两大类:求值(等式)和求最值(不等式),比方说上述题目给定的条件:给定了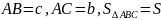 ,其实我们可以解三角形,求出三角形三个角度数或者是三角函数值,再求出第三条边长,这一系列求解过程都是“等式”下来,因为条件充足。比如:我们还知道确定一个三角形可以通过:1.两边及其夹角;2.两角。如果知道一个三角形的两边以及一个角(不是夹角,直角)不能够确定这个三角形,那么再求一些问题时,往往是最值(不等式)当然这里其实最多只有两种情况的三角形,但是可以说明,当条件不足时,问题往往是向“不等式式问题”的方向发展,正如上面所给的几个问题。
,其实我们可以解三角形,求出三角形三个角度数或者是三角函数值,再求出第三条边长,这一系列求解过程都是“等式”下来,因为条件充足。比如:我们还知道确定一个三角形可以通过:1.两边及其夹角;2.两角。如果知道一个三角形的两边以及一个角(不是夹角,直角)不能够确定这个三角形,那么再求一些问题时,往往是最值(不等式)当然这里其实最多只有两种情况的三角形,但是可以说明,当条件不足时,问题往往是向“不等式式问题”的方向发展,正如上面所给的几个问题。
其实在我们确定三角形时,解决上面的问题,可以看成是从正方向,也有很多时候是给定问题的答案让我们求解三角形,可以看成是反方向,而面对反方向时往往设出变量,走正方向的路,可以不难解决问题,利用这种思想,我们上述所给的题目其实也可以设置为“反方向”的问题,这里希望读者可以自行探讨,以便体验如何设置题目。
其实这种思想我们也可以利用n元线性方程组来理解:当给定一组增广矩阵秩为n的方程组,那么就有唯一的解,可以对应于“等式”,也就是具有确定性,用高中的思维其实就是条件充足可以求出确定的解;当系数矩阵的秩小于n时,那么方程有无数个解,一定程度可以说是具有不确定性(当然可以用基础解系来表示所有的解,这里理解的角度不同)对应于“不等式”,,用高中的思维其实就是条件不足,所给的解不确定。而且,设置题目的思想,其实可以这样理解:“正”:给定一个方程组让你来求解;“反”:给定一个方程组的解,但是不给全未知数(变量)的关系,让我们来设置一个或多个未知数之间的关系。
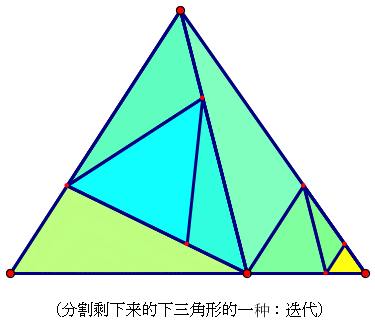
下面我们讨论二次分割的情况:(这里的二次分割是在指A点再引出一条线段,当然我们也可以在分割出来的三角形上继续做分割,那其实就有点向迭代的方向走了,和高中的题目的关系就不是很密切,但是我们在最后可以给出迭代后的图形)
做二次分割,张角定理我们也相应的进行推广,仍探讨分割线的长度,以及分割的角和分割的线段之间的关系。
如图:
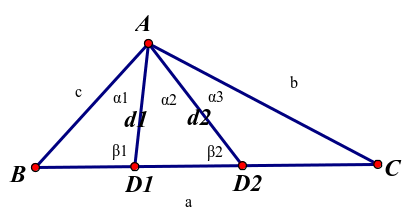
分割线变为两条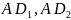 ,其他变量值如图所标
,其他变量值如图所标
利用同样的方法可以证明:在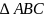 中:
中:
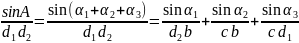
那么利用“算两次”的思想:在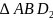 中:
中:
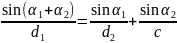
若已知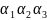 ,则可以利用上两式算出
,则可以利用上两式算出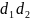 ,当然我们也可以在
,当然我们也可以在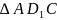 利用张角定理。
利用张角定理。
下面探讨分割的角和分割的线段之间的关系:
我们利用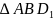 与
与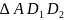 等高,底边比就等于面积比可得:
等高,底边比就等于面积比可得:
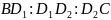 =
=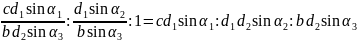
特殊情况:当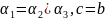 时,
时,
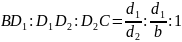 ,并且可以知道:当均分∠A时,并不能同时均分BC,当多次分割时,依然能得到这样的结论。
,并且可以知道:当均分∠A时,并不能同时均分BC,当多次分割时,依然能得到这样的结论。
通过上面我们还可以得到一些产物:
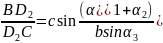
那么当二次分割时,我们依然是可以设置一次分割时类似的题目,这里我们不予赘述,读者可自行研究。
下面我们推广到N次分割,同样将张角定理进行推广,仍探讨分割线的长度,以及分割的角和分割的线段之间的关系。我们先来计算分割线的长度。
如图:
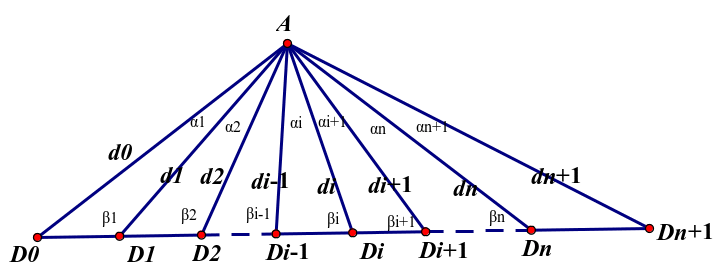
张角定理的推广:
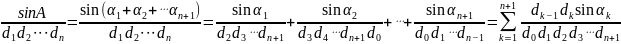
为了求出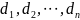 我们参照二次分割时的求法即可,n个未知数,利用n次张角定理列出n个“两两不等价”(这里所谓的“两两不等价”,我们可以用n元线性方程组它的系数矩阵的增广矩阵秩为n来理解。)的方程,便可求出
我们参照二次分割时的求法即可,n个未知数,利用n次张角定理列出n个“两两不等价”(这里所谓的“两两不等价”,我们可以用n元线性方程组它的系数矩阵的增广矩阵秩为n来理解。)的方程,便可求出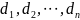 (这里不给大家细算)
(这里不给大家细算)
当然在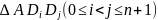 中使用张角定理可以得到相类似的结论。
中使用张角定理可以得到相类似的结论。
下面讨论在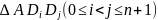 中底边的比。
中底边的比。
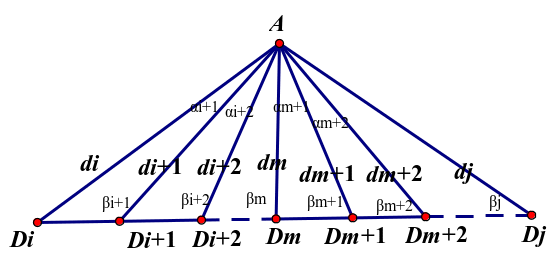
在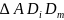 和
和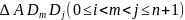 中分别关于βm使用一次正弦定理得:(当然使用面积比等于底边比快速)
中分别关于βm使用一次正弦定理得:(当然使用面积比等于底边比快速)
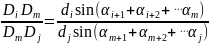
并且可以得到:
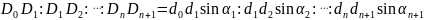
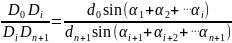
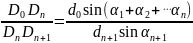
当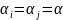 时,上述结论变为:
时,上述结论变为:

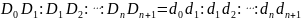
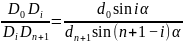
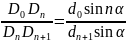
并且此时在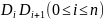 中线段相等的至多为两条.
中线段相等的至多为两条.
至此我们对三角形简单的分割做了简单的分析和探讨,了解了其中的分割而成的角与分割而成的线段之间的关系,本文也给出了几道高中相关知识的题目,涉及了向量(坐标思想),基本不等式,方程思想,甚至有数列的思想,对分割进行了某个方向的推广,本文的也对出题的角度做了简单的分析,分享了一些高中重要的思想方法:“算两次”等,同时也留下了一些问题供予读者思考。