(洛阳师范学院 数学科学学院,河南 洛阳 471934)
摘 要:对阶乘和双阶乘的历史及相关重要等式进行了简单总结,并通过实例研究了它们在级数中的一些应用.
关键词:阶乘;双阶乘;级数;斯特林公式
中图分类号:O173 文献标识码: 文章编号:
DOI:
前言
阶乘运算在组合学、代数和分析等课程有重要作用,以数学分析课程为例,在数列的收敛以及级数的收敛性等问题中会多次遇到阶乘运算,本文从阶乘符号发明的历史出发,通过具体实例,研究了阶乘的相关应用。
对于非负整数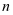 ,符号
,符号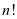 表示
表示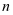 的阶乘,它是法国数学家Christian Kramp(1760-1826)在1808年首先引入的[1],定义为
的阶乘,它是法国数学家Christian Kramp(1760-1826)在1808年首先引入的[1],定义为
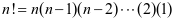
规定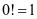 。当
。当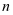 很大时,
很大时,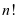 的数值是很大的。事实上,通过对
的数值是很大的。事实上,通过对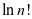 的放缩我们有如下逼近
的放缩我们有如下逼近
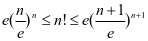
或直接使用Stirling逼近公式 (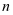 很大时)
很大时)
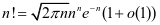 (1)
(1)
关于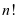 ,有很多著名的恒等式如
,有很多著名的恒等式如
欧拉数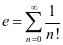 ,或
,或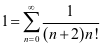
阶乘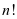 与Gamma函数
与Gamma函数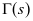 也有密切关系如
也有密切关系如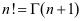 ,其中
,其中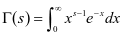 。此外在三角函数对应的泰勒级数中,更离不开
。此外在三角函数对应的泰勒级数中,更离不开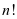 。
。
与阶乘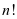 密切相关的一个概念是双阶乘
密切相关的一个概念是双阶乘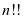 ,这个符号是1948年Merserve最先开始使用的[2],其定义为
,这个符号是1948年Merserve最先开始使用的[2],其定义为
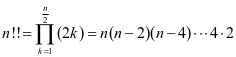 或
或 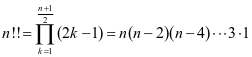
在著名的Wallis公式里,有
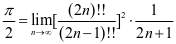
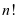 和
和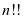 关系主要有
关系主要有
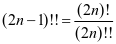 ,
, 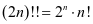
等,当然在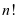 或
或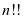 的运算中,
的运算中,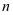 也可以不限于非负整数,甚至可以推广到复数,本文在此不再多述。
也可以不限于非负整数,甚至可以推广到复数,本文在此不再多述。
应用
例1 证明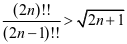 ,其中
,其中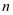 为非负整数。
为非负整数。
证明 对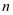 使用数学归纳法即可证明,详细证明略。
使用数学归纳法即可证明,详细证明略。
例2 判断级数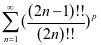 的敛散性。
的敛散性。
解 令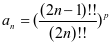 ,则
,则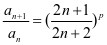 ,由于
,由于
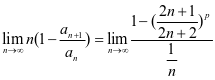
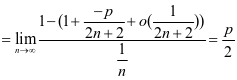
所以由拉贝判别法的极限形式知,当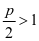 ,即
,即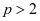 时原级数收敛,
时原级数收敛,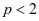 时级数发散。当
时级数发散。当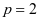 时,直接使用拉贝判别法也可证明原级数发散[3]。
时,直接使用拉贝判别法也可证明原级数发散[3]。
例3 判断级数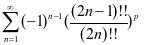 的敛散性。[4]
的敛散性。[4]
解 令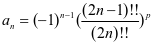 ,当
,当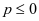 时,显然
时,显然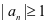 ,由于
,由于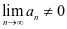 ,故
,故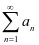 发散。
发散。
当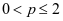 时,记
时,记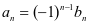 ,其中
,其中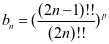 ,
,
由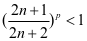 易知
易知
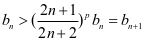
又由例1的结论知
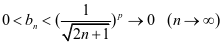
故由莱布尼茨判别法知原级数收敛。此时,由例2的结论知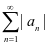 发散,于是,原级数当
发散,于是,原级数当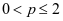 时是条件收敛的。当
时是条件收敛的。当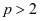 时,由例2的结论知,原级数绝对收敛。
时,由例2的结论知,原级数绝对收敛。
例4 求函数项级数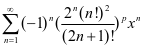 的收敛域。[5]
的收敛域。[5]
解 令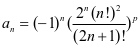
由于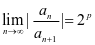 ,故收敛半径
,故收敛半径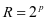 ,收敛区间为
,收敛区间为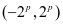 。
。
当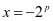 时,级数为
时,级数为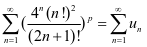 ,由于
,由于
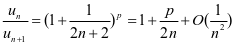
故由高斯判别法知,当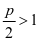 (即
(即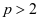 )时,级数
)时,级数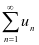 收敛,同时也是绝对收敛;当
收敛,同时也是绝对收敛;当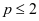 时,级数
时,级数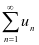 发散。
发散。
当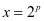 时,级数为
时,级数为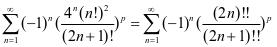 (2)
(2)
与例3的结论类似,当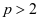 时,级数为绝对收敛;
时,级数为绝对收敛;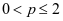 时,由(1)式,有
时,由(1)式,有
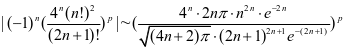
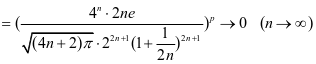
且
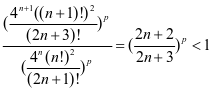
由莱布尼茨判别法知,级数(2)收敛,但由于其绝对值组成的级数发散,因此当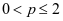 时,级数(2)条件收敛,当
时,级数(2)条件收敛,当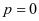 ,通项为
,通项为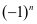 ,故级数为发散,
,故级数为发散,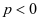 时,通项趋于无穷,因而级数也发散。
时,通项趋于无穷,因而级数也发散。
综上,原级数的收敛域当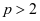 时为
时为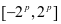 ,当
,当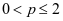 时为
时为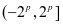 ,当
,当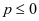 时为
时为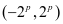 。
。
例5求函数项级数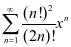 的收敛半径和收敛区间。[6]
的收敛半径和收敛区间。[6]
解 令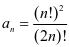 ,由
,由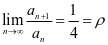 知,级数的收敛半径
知,级数的收敛半径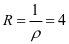 ,所以级数的收敛区间为
,所以级数的收敛区间为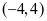 。
。
当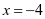 时,级数为
时,级数为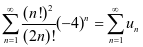 ,由(1)式得
,由(1)式得
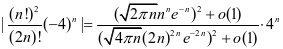
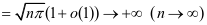
即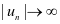 ,所以级数发散。
,所以级数发散。
当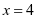 时,级数为
时,级数为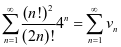 ,由于
,由于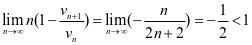 ,由拉贝判别法知,
,由拉贝判别法知,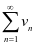 发散。故原级数收敛域为
发散。故原级数收敛域为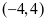 。
。
参考文献:
[1]Higgins, Peter. Number Story: From Counting to Cryptography[M]. New York: Copernicus, 2008:12.
[2]Meserve, B. E. Classroom Notes: Double Factorials[J]. The American Mathematical Monthly. 1948:55 (7): 425–426.
[3]华东师范大学数学系.数学分析(第四版下册)[M].北京:高等教育出版社,2010:16.
[4]费定晖,周学圣.数学分析习题集题解(4)[M].济南:山东科学技术出版社2001.100.
[5]费定晖,周学圣.数学分析习题集题解(4) [M].济南:山东科学技术出版社2001.246-248.
[6]华东师范大学数学系.数学分析(第四版下册)[M].北京:高等教育出版社,2010:54.
Research and Application
of the Factorial and Double Factorial in Series
Zhang Guo li
(College of Mathematics Science, Luoyang Normal University, Luoyang,471934,China)
Abstract: This paper briefly summarizes the history of factorial and double factorial and related important equations, and studies some applications in series by examples.
Key Words: factorial; double factorial; series; Stirling's approximation
—————————————
作者简介:张国利(1978-),男,焦作温县人,讲师,硕士,主要从事函数论、微分方程等方面的研究.