以定制动——动点轨迹问题的基本解题策略

以定制动——动点轨迹问题的基本解题策略

陈晓丽

浙江省绍兴市越城区文澜中学分部 312000

摘要:几何动点问题，看似千变万化，往往让学生“雾里看花”，在这类题的教学过程中，教师要引导学生，根据信息，抓住运动的本质，在运动过程中，抓住动点变量跟不动点之间的关系，做到一定制动。

关键词:动点轨迹问题，数学本质，以定制动

动点问题往往是让学生迷失方向的一类问题，似乎总是"剪不断，理还乱"。在动点轨迹问题的解题过程中，如何根据题意，抓住动点型题的本质？如何通过已知信息的分析找到动态过程种的不变量，以定制动，让运动轨迹浮出来？本文从动点轨迹类题的解题方法为例，对如何抓住动点类题的本质，体现数学学科的思维特点，谈谈自己的一点思考。

题型1：动中有定点、定线段

1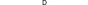 .如图,将矩形OABC置于平面直角坐标系xoy中，A( ,0), C(0,2),抛物线y=-x²+bx+c经过点B,C,顶点为D,将矩形OABC绕原点旋转一个角度θ，（0⁰<θ<360⁰），将得到的矩形OA'B'C',记A'C'的中点为E,连接DE，线段DE的长度最大值为。

解

思路分析：1.点E运动过程中，什么不变，运动轨迹是什么.

2.D、O、E三点什么时候距离最大.

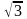：可以发现，旋转过程中线段点E到点O的距离不变，根据抛物线的对称性可知抛物的对称轴为直线X= ，所以解析式中的b=2 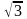，c=2，所以抛物线的解析式为y=-x²+2 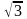x+2，点B的坐标为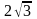（ ，2），点E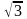（ ，1），点D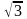（ ，5），所以OE=2，E点运动轨迹为右图所示的圆，当D、O、E三点在同一直线上时，DE取到最大值即为DO+OE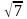=2 +2。

此类动点轨迹问题，存在动点到定点的长度为定值，找到这个定值，求出运动半径，问题也就迎刃而解了。

型题2、动中有定角、定线段

1.如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝4，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为。

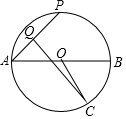
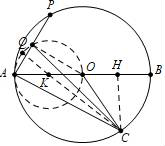
思路分析：1.随着点P的运动，点Q怎么运动，什么保持不变。

2.C、Q什么位置时达到最大值。

解：Q为AP的中点不变，所以OQ始终垂直AP,所以点Q的运动轨迹为以AO为直径的⊙K，⊙K的半径AK=OK=1，∠AOC＝120°,∠COH=60°，OC=2，所以OH=1，CH=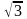 ,连接CK，勾股定理可得CK= = ,当点Q在CK的延长线上时，CQ的值最大为CK= +2

例2.如图，已知扇形AOB中，OA=3，∠AOB=120°，C是在 上的动点．以BC为边作正方形BCDE，当点C从点A移动至点B时，点D经过的路径长是________．（参考答案 提示:∠FDB为定值，轨迹为半圆O的中点H为圆心，HB为半径圆心角为∠GHB的圆弧）

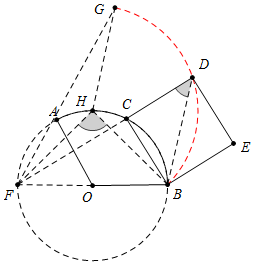
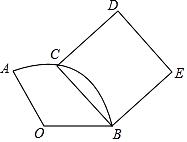
这类题目是最近中考中高频出现的题型，解题的关键在于找到运动中的不变直角，以及直角所对的定线段即轨迹所在圆的直径。

型题三、动中有定倍长

这类问题的动点跟不变量之间的关系隐藏的较深，学生需要仔细分析已知条件中的数量关系，才能发现隐含的数学本质，对学生有较高的能力要求，但是解题基本策略还是找出变化过程中不变的量与动点之间的关系。

1.如图，在扇形OCD中，∠COD=90°，OC=3,点A在OD上，AD=1，点B为OC的中点，点E是弧CD上的动点，则AE+2EB的最小值是 。

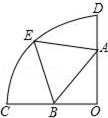
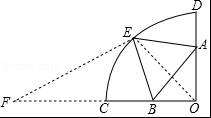
思路分析: 1.点E在运动过程中是否有不变量。

2.已知线段的长度跟结论要求的线段和之间怎么联系。

3.如何处理2EB这个倍值。

解：本题利用已知线段的数量关系，构建相似三角形，如图，延长OC至F，使得CF＝OC＝3．连结EF，OE，△OBE∽△OEF∴AE+2BE＝AE+EF即A、E、F三点共线时取得最小值即由勾股定理得AF＝ ＝

在解决动点与轨迹问题过程中，引导学生通过读动态图发现相关信息之间的联系，在运动和变化过程中找到变量与不变量之间的关系，是解动态图的基本策略，只有透过动态的表象，看到动态轨迹问题的实质，学生才解题才会会拨开云雾见日月。小而言之解题如此，大而言之，为人处世皆相通，我们只有抓住事物之间的本质联系，才不会被多态的表象所迷惑，所谓生活处处是数学，数学处处通生活。

参考文献:苏建强几何解题教学应突出三个关注点中学数学教学参考2019.04中旬[J]

孙琪斌图形运动路线及几何定值问题中学数学教学参考 2019 .1—2中旬[J]