福建省建瓯第一中学 353100
综合分析三角函数最值问题的解题思路方法,主要是通过将三角函数的函数值域性质落实到丰富的题目形式中,借以综合考察学生的基础知识、综合能力、数学思维。因此,想要熟练解决三角函数最值问题,必须要熟练掌握三角函数的相关图形和公式,逐步分析题目形式的意志条件和要素,举一反三总结解题的重要思路和方法。
配方法+换元法是指利用等式变形的手段,通过整体思想将三角函数进行变形转换从而求值。如果函数的表达形式为y=asinx+bcosx或y=sin2x+bsinx+c,即第一,函数形式为三角函数;第二,函数只包括正弦函数和余弦函数;第三,函数的最高次幂为2,则认为该函数满足条件,可以利用配方和换元的方式进行求解。
【例1】
现在已知函数y=sin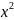 +acosx
+acosx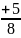 a-
a- 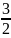 的最大值为1,求a的值。
的最大值为1,求a的值。
【分析】
结合题目的函数形式,已知其符合上述条件,首先,向着降低函数的次幂的方向思考,充分发散思维联想,利用已经学习过的同角三角函数的基本关系sin2x+cos2x=1进行整理转化并配方变形,使之成为只含有cosx或者sinx的二次函数,其次,向着三角函数的区间单调规律求最值的方向思考,利用属性结合的方式进行辅助处理,求值。
【求解】
解:y=sinx2+acosx+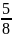 a-
a- 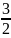
代入sin2x=1-cos2x
则y=1-cos2x+acosx+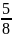 a-
a- 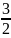
进行配方y=1-(cosx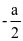 )2+
)2+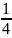 a2+
a2+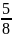 a-
a- 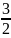
因为-1 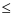 cosx
cosx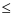 1
1
所以
(1)当-2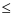 a
a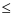 2时,
2时,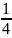 a2+
a2+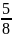 a- -
a- -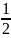 =1
=1
则得出a=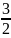 或a=-4(舍)
或a=-4(舍)
(2)当a<-2时,-(-1- 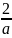 )2+
)2+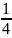 a2+
a2+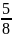 a-
a- 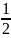 =1
=1
则得出a=-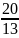
(3)当a>2时,-(-1- 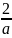 )2+
)2+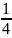 a2+
a2+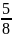 a-
a- 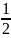 =1
=1
则得出a=- 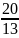 (舍)
(舍)
答a=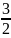 或者-
或者- 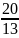
【例2】
现在已知有函数 y=sinxcosx+sinx+cosx求解其最大值。
【分析】
结合题目的函数形式,已知其符合上述条件,首先,向着降低函数种类的方向思考,利用相关公式进行换元,将sinx+cosx、sinxcosx均用t表示使其成为仅包含t的一元二次函数,其次,向着一元二次函数单调性求最值的方向思考,利用相关公式,求值。
【求解】
解:假设sinx+cosx=t(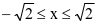 )
)
且sinxcosx=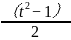
代入y=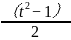 +t
+t
化简得y=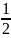 t2+t+
t2+t+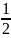
当t=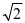 时
时
则得出ymax=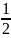 +
+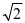
三角函数的有界性是指y=sinx或y=cosx的y值随着x值的变化而变化且变化范围为-1≤y≤1(此处建议利用正弦函数或余弦函数的函数图像进行分析则更加清晰)。如果函数的表达式为y=asin2x+bsinx+c(a≠0)、y=asinx+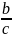 sinx-d、y=acosx+
sinx-d、y=acosx+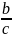 cosx-d ,即第一,函数形式为为三角函数;第二.函数只包括sinx或cosx,则认为该函数满足条件,可以利用三角函数的有界性进行求解最值。
cosx-d ,即第一,函数形式为为三角函数;第二.函数只包括sinx或cosx,则认为该函数满足条件,可以利用三角函数的有界性进行求解最值。
【例3】
现在已知函数y=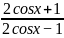 ,求解其y的值域。
,求解其y的值域。
【分析】
结合题目的函数形式,已知其符合上述条件,首先,分析该函数结构分子分母三角函数同名同角,其次,转化该函数形式并利用三角函数的有界性进行求解。
【求解】
【方法一】
解:y=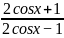
变形y=1+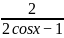
因为-1≤cosx≤1,也即|cosx|≤1
所以y≥3或y≤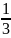
【方法二】
解:y=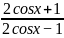
变形cosx=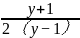
因为-1≤cosx≤1,也即|cosx|≤1
即|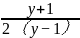 |≤1,
|≤1,
所以y≥3或y≤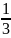
不等式法是指利用不等式变形的手段从而求值。如果函数的表达形式为三角函数不等式,则认为该函数满足条件,可以利不等式法进行求解。
【例4】
现在已知函数y=2cos2x·sinx且有自变量x∈(0,π),求函数的值域。
【分析】
结合题目的函数形式,已知其符合上述条件,因为自变量知x∈(0,π),结合三角函数图像可知因变量y≥0。
【求解】
解:因为x∈(0,π),y≥0
则y=2cos2 x·sinx
y2=4cos4x·sin2x
=2(1-sin2x)(1-sin2x)2sin2x≤2(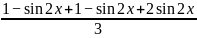 )3
)3
=2(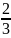 )3
)3
=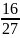
当1-sin2x=2sin2x
则sinx=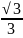
ymax=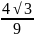
所以函数的值域为0≤y≤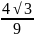
数形结合法通常是指利用函数图像和函数对照结合的方式,将抽象的函数变化关系进行直观的转化和分析,从而帮助对题目进行分析理解和快速解答。如果函数的表达式为y=
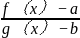 ,可以转化为动态的A(g(x),f(x))点和静止的B(b,a)点的相互关系问题,则认为该函数满足条件,可利用数形结合的方式进行解答。
,可以转化为动态的A(g(x),f(x))点和静止的B(b,a)点的相互关系问题,则认为该函数满足条件,可利用数形结合的方式进行解答。
【例5】
现在已知函数y=2+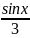 +cosx,求其ymax和ymin。
+cosx,求其ymax和ymin。
【分析】
结合题目的函数形式,已知其符合上述条件,利用数形结合的方式,首先,向着已知函数的方向,进行等式变形y=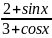 =
=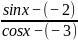 ;其次,向着数形结合的方向,将其转化为点A(-3,-2)连接点 B(cosx,sinx)直线斜率。
;其次,向着数形结合的方向,将其转化为点A(-3,-2)连接点 B(cosx,sinx)直线斜率。
【求解】
解:已知y=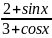
=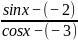
是过点A(-3,-2)的圆的切线。
已知圆x2+y2=1的切线为y=kx±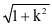
则过点A(-3,-2)的圆的切线为-2=-3k±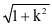
可得k=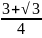
所以ymax=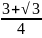
ymin=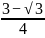
综合全文可知,全面分析三角函数最值问题,是高中数学重要知识和工具,蕴涵着关键的划归与转化的数学思想,从而学生能够掌握其精髓,提升数学思维。因此,我们必须要彻底认识三角函数最值问题的本质特征,系统思考三角函数最值问题的解决思路,熟练掌握,综合提升,帮助夯实坚实全面的数学素养。
李敏,严忠权,莫晓辉.核心素养核心素养视域下对数学思想方法的思考——以函数为例[J].教育观察,2020,9(43):56-59.
肖桂宏.三角函数最值问题的基本题型分析[J].中国高新区,2018(11):98.
张建凤.从历年考点分布看高考数学复习[J].延边教育学院学报,2015,29(01):119-123.
凌广燕.浅析三角函数最值在解题中的理论与实践思考[J].科技风,2014(21):183.
王洁.高考三角函数题型探析[J].甘肃联合大学学报(自然科学版),2012,26(S4):50-52+54.