二次型的几个应用实例

二次型的几个应用实例

傅小兰

江汉大学人工智能学院，湖北、武汉 430056

二次型是线性代数中的一个重要知识点，其在数学、物理和力学中都有着广泛应用。二次型的应用在高中数学知识中就有体现，如用坐标变换把圆锥曲线、双曲线、抛物线化为标准曲线的实质是将二次型进行标准化。事实上，二次型在证明不等式、分解多项式的因式、求解二次函数最值以及计算定积分中都有重要应用。

1、用二次型证明不等式

一个实二次型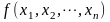 是正定的，若其对任意的实数 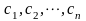，都有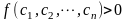 。可以通过构造正定二次型，利用其正定性来证明不等式[1]。

例1：证明不等式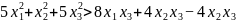 恒成立。其中 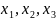不全为0。

证明：将不等式移项得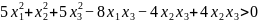 。令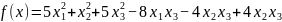 ，则我们只需证明f(x)恒大于0即可。可知f(x)是一个实二次型，其二次型矩阵的三个顺序主子式均大于零。因此，f(x)是正定二次型。因此，对于任意一组不全为0的数，都有f(x)>0，即证。

2、二次型在二次曲线中的应用

二次型起源于将二次曲线或二次曲面方程变型为标准型，所以二次型在二次曲线中的有最基本的应用。因为二次曲线方程经可逆线性变换后的方程所对应的二次曲线图形与原图形是全等的即既不改变曲线的形状，又不改变大小。因此，我们在判断二次曲线的形状时，可利用正交线性变换先把二次曲线化为标准型，然后再来判定原二次曲线的形状。

例2：判断二次曲线方程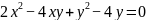 的形状并求其面积。

解：为了使方程所有项全部都是二次项，我们再设一个变量z。令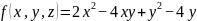 z，此时有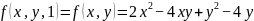 。将此二次型的矩阵做正交变换使其化为对角矩阵diag(4,1,-2)。对角矩阵所对应二次型为 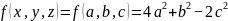。由于正交变换不改变二次曲线的形状和大小，则有 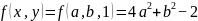，进一步将其整理得 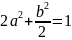。很显然，这是一个椭圆方程。长短轴分别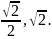为 面积为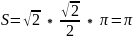 ，即原二次曲线方程的形状为椭圆，面积为π。

3、二次型用于因式分解

因式分解是初等数学中很常见的一类问题，它在解方程，求多项式的根等问题上能一定程度上简便运算过程。由于二次型都是二次齐次多项式，我们在这里只讨论二次多项式的因式分解。应用下面的定理，我们能直接判断给出的二次多项式是否可以分解成几个一次多项式的乘积。这给多项式的因式分解提供一种强有力的解题思路[1]。

定理：[2]设f为实数域上的二次型，则f可分解为实数域上的两个一次齐次多项式乘积的充要条件为f的秩为1或者f的秩为2且符号差为0。

例3：试判断多式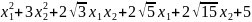 能否在实数域上因式分解。若可以，请分解。

解：令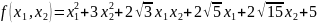 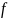， 存在一次项和常数项，可根据多项式的特征构造出下列二次型，

。

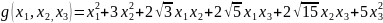则有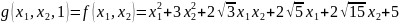

进一步将二次型写成矩阵形式 。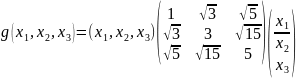

二次型矩阵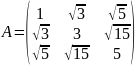 ，易知A的秩为1。根据上述定理，可得 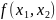能在实数域范围内进行因式分解，即 。

4、二次型用于求解在函数最值

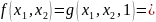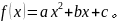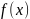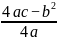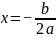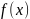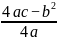在函数求最值的问题上，一元二次函数是一个很熟悉很常见的数学模型。给出一个一元二次函数 当a>0时， 有最小值 ，此时 。当a<0时， 有最大值 ，此时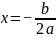 。下面将探究多元二次函数是否同样存在类似的结论。

令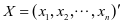 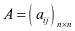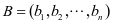， ， ，则多元二次函数的一般形式为 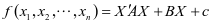。再作线性变换 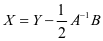，可得

。

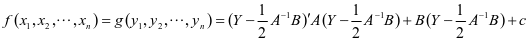化简上式得 。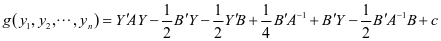

最后化简，可以得到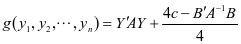 。故当A为正定二次型时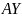， 也是正定二次型。根据正定二次型的性质，我们有 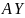大于或等于零始终成立。故 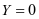，即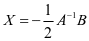 时，函数最小值为 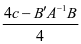。[3-5]

5、二次型计算定积分

下面介绍运用二次型，可以不用通过求原函数，而通过直接求出所积函数的面积给计算定积分。由于二次型的正交变换是不改变原图形的大小及形状的，因此可应用正交变换，使原图形面积更直观的体现出来，为解决定积分问题提供了一种可行的简便方法[10]。

例4：求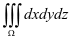 的值，其中 。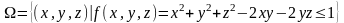

解：二次型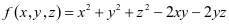 的矩阵为 。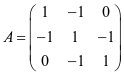

可由正交变换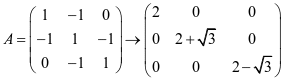 ，得标准型。这表明原椭球与新椭球 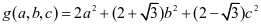的体积相同，故原积分值为 。

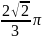参考文献：

[1]白颉.二次型理论在中学数学中的应用[J].太原大学教育学院学报，2010(1):113-115.

[2]王萼芳.高等代数（第四版）[M].北京：高等教育出版社，2015.

[3]徐阳栋.二次型在多元函数极值问题上的应用[J].教育教学论坛，2015(28):180-181.

[4]杨桂元.二次型的正定性在函数极值判定中的应用[J].数学理论与应用，2007(1):21-23.

[5]陈荣群.二次型在求条件极值中的应用[J].福建教育学院学报，2008(10):100-101.