漫谈微积分中的数学美

漫谈微积分中的数学美

曾令龙

（黔南民族师范学院数学与统计学院  贵州都匀  558000）

摘要：本文探讨微积分中的数学美，介绍微积分中数学美的主要形式。在微积分的教学过程中。若能从审美的情趣、鉴赏的角度进行阐述，将有助于学生理解、掌握微积分的精髓要义，这对引发学生数学美的好奇、培养学生的数学素养具有重要意义！

关键词：微积分  数学美  统一美  实用美  形式美  对称美  奇异美

引言：数学是理性思维和想象的结合，是研究数量关系、几何结构、运动变化以及空间模型等概念的一门科学。透过抽象化、符号化、逻辑推理的使用，由计量、计算、度量和对物体形状及运动的观察中产生，它的建立、发展源于社会的需求，服务于社会需要，所以就有了数学美。微积分作为数学中浓墨重彩的篇章，处处彰显数学之美，从微积分诞生、演变、发展的脉络来看，都蕴含深厚的美学思想，具有独特的美学价值。它美在统一、在实用、在形式；也美在对称、在奇异，本文将从这几点对其进行探析。

1  统一美

极限是学习微积分必须掌握的核心概念，微积分中，无论是微分，还是积分，最终都会统一到极限的层面。例如函数在区间，上定积分的定义：

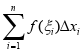，就将定积分统一到了求积分和的极限；又如函数在某一点的导数：，函数的导数：，就将函数在某一点的导数或函数的导数统一到了求函数在某一点处的平均变化率的极限或求函数在任一点处的平均变化率的极限。

不定积分是求导的逆运算，是求被积函数的所有原函数的集合，而定积分则是某种特殊和式的极限。定积分、不定积分看似毫无关联，但牛顿-莱布尼茨公式“若函数在，上连续，则在，上可积，那么：

，其中”实现了内涵不同的两者之间关系上的统一，从而将定积分的计算转化为求的原函数在区间，上的增量，大大简化了定积分的计算。

例如求在区间，上，以正弦曲线为曲边的曲边梯形的面积。若根据定积分的定义计算则十分繁难，非常不易，而用牛顿-莱布尼茨公式计算就相当简便。

在区间，上连续，故其在，上可积，由定积分的几何意义知，所求面积为：

万河奔流同入海，其它积分如二重积分、三重积分、曲线积分、曲面积分等的计算也有曲工异同之处，彰显了微积分在整体上的统一。

2  实用美

自微积分这门学科诞生以来，无是理论研究还是社会实践，其在社会发展中都扮演着不可或缺的重要角色。微积分作为数学的重要基础理论，除了在本学科之外，其在物理学和经济学领域中的广泛应用也人人谐知、有目共睹，取得了辉煌成就，海王星、黑洞的发现就是数学理论发挥无比威力的例证之一。

高中物理中许多公式或定理就体现微积分的实用美。如瞬时速度：；瞬时加速度：；磁感应强度：等，这些公式简单明白，便于记忆。微积分运用在物理学中，能更好的表达所要反映的物理现象、规律，也让人容易理解。

微积分在经济学中的应用有一个典型的例子，就是解决利率问题。设本金为，本息为，年利率为，则年后的本息为，假如把一年分次来计算利率，则每期利率为，年后的本息为，当时，，于是本息与本金之间的关系可表为；。

微积分的实用性绝不止以上两个领域，它的实用性几乎渗透到了自然科学与社会科学的每一个领域，成为我们解决实际问题不或缺的有力工具。

3  形式美

微积分符号的重复运用和符号的简洁是微积分形式美的体现。函数的一阶导数记作或，二阶导数记作或，或就表示其阶导数；求函数的定积分，就记作；当自变量增加时，我们只需将积分符号依次排在前面，后面再加上对某个变量的微分即可。如函数，的二重积分，记作，，函数，，的三重积分记作：，，等等，形式上的美，一目了然，简洁明白，使人愉悦，便于记忆。

其次，微积分中的公式本身就是形式美的表现。它美就美在可将看似毫无关联的知识在微积分公式的作用下进行相互转化，例如我们在数学分析中学习过的的格林公式：，它美在可以使闭区域内二重积分与在边界的一重曲线积分进行互相转换；再看高斯公式：假定有一空间中的闭区域，并且区域的表面是分片光滑的，其中的三个三元函数分别为，，，这三个函数及一阶偏导数在上连续，则：

。高斯公式的美妙之处在于将三重积分（体积分）与二重闭合曲面积分相结合，并实现互相转化，其在向量场和梯度理论中有广泛应用。

4  对称美

万千世界中，美与对称息息相关，紧密相连，对称美给微积分增添了一抹亮丽的色彩。

谈及对称，我们会想到对称区间，由对称区间就联想到函数的奇偶性，若被积函数有奇偶性时，积分就会变得简单许多。给出对称区间，上的某个偶函数，其在该区间内连续，把区间，分成，和，两个子区间，根据定积分对区间的可加性知：，这便达到了事半功倍的效果。对于奇函数，利用对称区间的特点，同理可得。

微分学中，我们知道奇函数的导数是偶函数，若，，设为奇函数，则有。对这个等式两边同时求关于的导数，且令，那么，即，所以为偶函数；同理可知偶函数的导数是奇函数。连续有左连续与右连续，极限有左极限与右极限，导数有左导数与右导数，确界有上确界与下确界等等，它们都把微积分的对称之美表现得淋漓尽致。

5  奇异美

有种特殊的美叫奇异美，它往往会引起人们无穷想象，激发人们对它进行探索研究。

我们知道，，它们都是无理数，如何求它们的近似值呢？

对于无理数，首先会想到指数函数，利用泰勒公式展开该函数，并求其麦克劳林级数，可得，若令，就可得的展开式为：，利用该式即可求出的近似值。

对于的近似值，可通过傅里叶级数将函数在区间，内展开为余弦函数来求，具体步骤如下：

将作周期为2的偶延拓，得一连续的延拓函数。

，，，，…，

由收敛性定理，在区间，内，

当时，因延拓函数连续，所以上式右端收敛到，所以

，，故用此方法来求的近似值，过程虽复杂了些但其收敛速度较快。

以上将无理数与展开成了有规律的展式，神奇之处在于将无理数表为无穷多个有理数之和，利用功能强大的电子计算机便可求出它们的近似值，且可以达到任意的精确度要求，解决了初等数学难以完成的事情，充分展示着微积分的奇异美。

微积分的奇异美无处不在，从某种角度上来讲，抽象的美也是奇异美。如极限就给我们无限想象的空间，《庄子 天下篇》中的“一日之棰，日取其半，万世不竭”便是例证。

极限的本质是无穷逼近，如数列的极限：的含义是：无论事先给定的正数多么小，总存在正整数，当＞，都有＜，这就是说在无限变大的过程中，可以任意变小，要多小就有多小。

再如我们学过的狄利克雷函数同样让人产生无限遐想，它有具体的函数表达式：，该函数在实数集中处处不连续，其图像客观存在，但确无法画出，这给人一种只可意会不可言传的奇异美感。

总结：兴趣是最好的老师，学习的生涯，道阻且长。倘若在微积分的学习过程中，能充分挖掘微积分中的数学美，体会其独特的美学思想、美学价值，从美的角度赏析微积分，而不是以一种复杂的心态去看待，就能激发学生对数学的热情和求知欲，从而开阔视野、拓展眼界，这对提高学生的数学素养至关重要！

主要参考文献

[1]华东师范大学数学系编：数学分析（上册）[M]，北京高等教育出版社，2010年第四版

[2]黄永彪，杨社平：微积分基础[M]，北京理工大学出版社，2012年第一版

[3]张长勤 吴坚. 新技术背景下微积分课堂教学的思考[J]，安徽农业大学学报:社会科学版, 2014（23）:126

[4]黎琼，LI，Qiong(East，China，Institute，& of等) [J] (2011)，微积分发展史. 科教导刊(上旬刊)

[5]白文莲，微积分给予的启示[J]，科学教育，2006，012（001）:54—55

[6]曹桃云. 微积分中蕴含的数学美[J], 成都大学学报:教育科学版，2007（07）：53—55

1