双流中学九江实验学校 610200
【摘要】本文从初中学生在直角三角形存在性问题的困难入手,结合初中学生的对图形知识的掌握情况,通过多种解题的方法手段,将提高学生的直角三角形存在性问题的解决能力,激发学生对于数学学习的兴趣,增强学生的几何直观,从而提升学生的逻辑推理,直观想象等素养。
【关键词】初中数学;直角三角形;基础教育;
一、引言
相比小学的学生而言,初中学生有一定的几何图形基础能力,在三角形方面,他们已经有更加深入的钻研。但就基础教育课程而言,初中学生通常就存在性问题显得较为薄弱,尤其是特殊的三角形存在性问题,几乎都是他们的短板或噩梦,绝大部分初中生都存在着对动点不熟悉,理解困难等问题。
二、初中学生动点问题难点分析
数学作为一个理学科目,整体对学生的逻辑要求偏于抽象,这让部分初中学生对数学几何部分知识无法形成直观的印象,形成了长时间来困扰数学教学的一个问题。因此,我们想呈现多种解决方法,让学生能找到一种自己能够容易理解的方法,将抽象的知识点问题与公式定理转化为多种方法的表达[1]。或许就能使得学生对动点问题燃起更多一点的兴趣。让学生感受一题多解的魅力,这也是笔者在教学中所希望的。
三、动点引起的直角三角形存在性问题
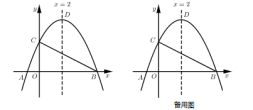 例题:如图,在平面直角坐标系中,抛物线
例题:如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,连接BC,
与x轴交于点A、B,与y轴交于点C,连接BC,![]() ,对称轴为
,对称轴为![]() ,点D为此抛物线的顶点.
,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
【答案】(1)![]() ;(2)(7,4)或(-3,
;(2)(7,4)或(-3,![]() )或(3,
)或(3,![]() )或(3,4).
)或(3,4).
【解析】解:(1)∵抛物线![]() 的对称轴为
的对称轴为![]()
∴a=![]() ,即
,即![]() ,
,
∵OA=1,A在抛物线上,
则将A(-1,0)代入![]() 得:c=
得:c=![]() ,
,
即抛物线的解析式为:![]() .
.
(2)由(1)知,抛物线对称轴为x=2,设P(2,m),Q(x,y)
若以B、C、P、Q为顶点的四边形为矩形,
则△BCP为直角三角形
在![]() 中,当y=0时,x=-1,x=5;当x=0时,y=
中,当y=0时,x=-1,x=5;当x=0时,y=![]() ,
,
即B(5,0),C(0,![]() ),
),
四、直角三角形存在性问题一题多解
下面我将从勾股定理,相识三角形,三角函数三个方法来解决例题的问题,从多知识点,多方面提供学生探讨问题的方法。
方法一:勾股定理
分类讨论:
①当![]() =
=![]() ,
,
即25+![]() =32+
=32+![]() +22+
+22+![]()
解得:m=4或m=![]() ,
,
即P(2,4)或(2,![]() ),
),
此时PQ为对角线,BC为对角线,
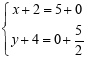 或
或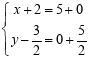
则Q(3,![]() )或(3,4).
)或(3,4).
②当![]() =
=![]() +
+![]() ,
,
即32+![]() 25+
25+![]() +22+
+22+![]()
解得:m=![]() ,即P(2,
,即P(2,![]() ),
),
此时BP为对角线,CQ为对角线,
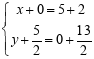
则Q(7,4)
③当![]() =
=![]() +
+ ![]()
即22+![]() =25+
=25+ ![]() +32+
+32+![]()
解得:m=-6,即P(2,-6),
此时CP为对角线,BQ为对角线,
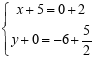
则Q(-3,![]() )
)
综上所述,Q点坐标为(7,4)或(-3,![]() )或(3,
)或(3,![]() )或(3,4).
)或(3,4).
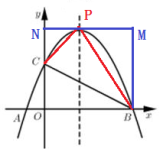 方法二:相似三角形
方法二:相似三角形
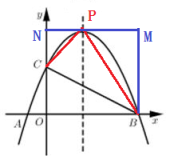
分类讨论①当∠CPB=90°时,如图,过P作x轴的平行线,交y轴于N,过B作BM⊥PN于M
易证:△PNC∽△BMP
∴![]() 即
即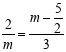 ,
,
解得:![]() 或
或![]() ,
,
即P(2,4)或(2,![]() ),
),
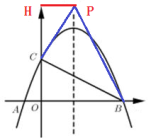 ②如图,当∠PCB=90°时,
②如图,当∠PCB=90°时,
过P作PH⊥y轴于H,
同理可得:![]() ,
,
 即
即 ,解得:
,解得:![]()
即P(2,![]() )
)
③当∠CBP=90°时,如图所示,
同理知,![]() 即
即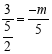 ,
,
解得:m=-6,即P(2,-6)
再由方法一中的方法求得Q点坐标即可;
 方法三:三角函数
方法三:三角函数
分类讨论
①当∠CPB=90°时,易知∠NCP=∠BPM,
∴tan∠NCP= tan∠BPM
即 ![]() 即
即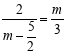 ,
,
 解得:m=4或m=
解得:m=4或m=![]() ,
,
即P(2,4)或(2,![]() ),
),
②如图,当∠PCB=90°时,
同理可得:tan∠PCH=tan∠CBO,
 即
即![]() ,即
,即 ,解得:m=
,解得:m=![]()
即P(2,![]() )
)
③当∠CBP=90°时,同理知,![]() ,
,
即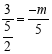 ,解得:m=-6,
,解得:m=-6,
即P(2,-6)
再由方法一中的方法求得Q点坐标即可.
五、总结
从数学意义上讲,几何问题一个宁人向上的学问,而动点问题则是通过观察几何的变化,发散想象,分类总结提炼出结果。常言道,数学源于生活而高于生活。正是生活中充满各种图形,需要我们去研究探讨。几何动点问题孕育了几何数学教育的内涵,通过教师本身的经验与知识逻辑框架,建立起多种层次的数学解题方法[2],最后回馈于学生。把数学作为内核,将知识融入学生的思想。
而正是由于一题多解的方式的运用,许多学生对于数学的畏难情绪发生了转变,越来越多的学生乐于发现不同方法解决同一问题,对数学学习的兴趣也浓厚了起来。这样的变化是可喜的,这说明学生将自己的成就感与方法的多元化得分配到研究数学知识上,在这样的过程当中,不仅凝炼了学生的分类思想,又掌握了数学的知识,两者相辅相成,达到了一种和谐的统一[3]。
道家有言,世间万物,一生二,二生三,三生万物。正是这样的相互促进,共同提高,让学生能够全面发展,而又是这样的发展,使得学生越变越好,正是切合教育的初衷。不得不说,这样的方式,以其圆润的循环,扩大和提高了学生能力的同时,又使得学生掌握知识,发散兴趣,最终提升学生的数学核心素养。而一题多解这样的益处不仅是数学这一科目,更能够发散到其他课程。
参考文献:
[1]周雁春.巧用一题多解拓宽解题思路[J]. 甘肃教育, 2011(06).
[2]王宜田.浅谈数学解题教学中的一题多解[J].科技信息:学术研究,2008(14).
[3]刘永生.数学思维的发展[D].华中师范大学.2004(02)
![]()