整体换元在复合函数问题中的关键应用

整体换元在复合函数问题中的关键应用

吴谱文

阜阳市城郊中学   安徽省 阜阳市   236000

摘要：引导学生正确使用符号语言清晰地刻画函数的性质，掌握复合函数的构成、运算法则和变化规律，体会整体换元在解决复杂函数问题中的重要性，学会引入新的变量降低复杂函数解决的思维梯度，简化函数形式，抓住函数本质，总结函数问题解决的数学思想与数学方法，对提升数学抽象、数学运算、逻辑推理等数学学科核心素养有着重要意义与价值。

关键词：函数，换元，复合，变量，分解

引言：函数是贯穿高中数学课程的主线，其中复合函数更是函数学习研究的主要载体。首先，教材在介绍指数函数、对数函数、幂函数、三角函数等基本初等函数时，学生理解不难，但是对通过多种运算法则复合而成的复杂函数的理解存在很多困惑。其次，整体换元法在函数性质的研究中是一个经常运用到的、典型的数学方法，在解决复合函数问题中起到了很关键的作用。并且高考对于复合函数考查类型多样，主要围绕函数的基本性质，所以笔者在这里是以初等函数为基础，围绕复合函数的基本性质进行探究的。

换元的实质是转化，关键是构造元和设元，理论依据是等量代换，目的是变化研究对象，将问题迁移至新对象的知识背景中去研究，从而使非标准问题标准化，复杂问题简单化，变得容易处理。[1]

高中数学中换元法主要有以下两类：

第一，整体换元：以“元”换“式”。

第二，三角换元：以“式”换“元”。在这里笔者所讲的是整体换元。

在高中数学函数学习中，复合函数是重点也是难点。复合函数是由简单的若干个初等函数通过多种运算法则复合而成的复杂函数。一般地，对于两个函数和，给定的一个值，就得到了的值，进而对应了的值，这样其实就是的函数，我们称这个函数为函数与的复合函数，记作.其中为中间变量.简单来说就是。是函数值，而每一个值又同时是的作用对象。例如函数，可以看成与复合而成。

这里主要介绍较为简单的复合函数，由内外函数复合而成，两个变量，,其中是自变量，是因变量。复合函数中符号和分别表示两种对应关系，可以是线性关系也可以是非线性关系。在此之前我们所学习到的函数都给出了具体的解析式，如正比例函数、反比例函数，指数函数、对数函数、幂函数、三角函数等，而复合函数这种抽象的表达方式，学生在理解上还存在一定的困难。所以在复合函数的学习中我们经常运用到化归与转化的思想来解决这类问题。在研究和解决有关数学问题时采用整体代换将问题通过变换使之转化，将一个复杂的问题转化成熟悉的，能够解决的或已经学习过的问题进而达到解决的目的。高中数学学习中复合函数的学习主要有以下几个方面：

一、复合函数定义域

定义域作为函数三要素之一，重要性不言而喻。在北师大版高中数学教材必修一中开始学习，是整个高中阶段函数学习的重点，也是高考常考点。定义域是指使得函数解析式有意义的自变量取值范围的集合。在这里强调一下，定义域是集合，很多学生保留不等式形式是不符合要求的。很多学生在定义域方面失分是因为定义域概念没有理解。其主要根据是

(1)分母不为零；

(2)偶次根号下的被开方部分为非负；

(3)对数式中的真数部分要大于0；

(4)指数函数和对数函数的底数大于0且不等于1.

如果是抽象函数，特别是复合函数中某一对应关系抽象成一个或者表示时去求定义域，学生就不容易理解，更不要去解决问题了。

抽象函数定义域的求解关键是要找到对应关系的作用对象。在高中数学函数学习中自变量大多是表示，当然自变量的符号表示并不是唯一的。对于与，前者定义域的求解是没有问题的，而后者很多学生就搞不清作用对象是呢还是这个整体，很多学生在这里分辨不清，很困惑，导致经常错解。根本原因还是函数概念没有掌握透彻。其实，表达式中的是自变量，是对应关系的作用对象，强调对应关系和作用对象。而后者是复合函数的范畴，此时的作用对象是这个整体，高中数学所讲的抽象函数定义域问题偏向于与复合函数结合的问题。

1.已知的定义域，求的定义域.

例1.已知函数的定义域为，求函数的定义域.

解 由函数定义域为，所以

   所以有，解得

所以函数的定义域为.

2.已知的定义域，求的定义域.

例2.已知函数的定义域为，求函数定义域.

解  由函数定义域为，所以

所以有，

所以函数定义域为.

3.已知的定义域，求的定义域.

例3.已知函数的定义域为，求函数定义域.

解  由函数定义域为，所以

所以有，则

解得

所以函数定义域为.

总结：求解抽象函数得定义域主要抓住两点：

（1）函数定义域是指自变量的取值范围的集合；

（2）同一对应关系的作用对象范围是一样的；

教学过程中，针对套用复合类型要注意“从外到内”依次限定的分析方式，强调给学生“由外到内”的分析思想，结合函数的定义及性质，更好的解决复合函数定义域问题。[2]

二、复合函数导数

复合函数的导数为

         .

例4.求函数的导数.

解  引入中间变量，则函数是由函数与复合而成的.

查导数公示表可得.

根据复合函数求导法则可得

    .

例5.求函数的导数.

解  引入中间变量，则函数是由函数与复合而成的.

查导数公示表可得.

再由复合函数求导法则可得

    .

总结：复合函数导数求解，首先需要掌握复合函数的结构，其次将复合函数分解成若干个初等函数，最后由复合函数求导法则求出导函数.

三、值域或最值

例6.求出函数在区间上的值域.

解： 函数变形为

换元，所以得

配方得

函数在上先单调递减后单调递增,

当时，取得最小值，当或时，取得最大值.

所以函数在区间上的值域为.

例7.求出函数在上的最大值与最小值.

解  换元.由，得出

所以函数化简为

因为函数的递增区间是，

所以函数在上单调递增。

当时，取得最小值，当时，取得最大值.

总结：求复合函数的值域或最值时，首先需要掌握复合函数由哪些初等函数复合而成，其次可将内函数或某个整体引入变量进行整体换元，需要注意的是在换元时需要求出新的未知元的取值范围，最后结合函数单调性求出新的函数的值域或最值，也就是原复合函数的值域或最值.

四、复合函数单调性

形如的复合函数的增减性如下：

复合函数单调性的规律是“同增异减”

例8.求函数的单调递增区间.

解 由，解得或.

设，则为增函数.

根据复合函数单调性的规律是“同增异减”要求函数的单调递增区间，即求函数的单调递增区间。

函数的单调递增区间为

函数的单调递增区间为.

例9.求函数的递增区间.

解  设.

因为函数的递增区间是，由

         ,

得        ，

所以，函数的递增区间是

例10.求函数的递减区间.

解  设.

因为函数的递减区间是，由

得        

所以，函数的递减区间是

.

总结：讨论或判断复合函数单调性的关键在于掌握复合函数都是由哪些基本初等函数构成，然后引入中间变量，分别分析内外函数的单调性，按照复合函数单调性的同增异减规律，最后得出单调性.

五、复合函数零点

对于函数，把使的实数叫做函数的零点。

复合函数零点问题的特点：考虑关于的方程根的个数，在解此类问题时，要分为两层来分析，第一层是解关于的方程，观察有几个值使得等式成立；第二层是结合着第一层的值求出每一个值被几个对应，将的个数汇总后根的个数。

求解复合函数零点问题的技巧：

（1）此类问题与函数图像结合较为紧密，在处理问题的开始要先作出，的图像。

（2）若已知零点个数求参数的范围，则先估计关于的方程中解得个数，再根据个数与的图像特点，分配每个函数值被几个对应，从而确定的取值范围，进而决定参数的范围。

例 11.求出函数的零点个数

解 函数零点的个数可转化为对应方程实数根的个数求解，把看成一个整体，即 ，则可得方程

解得,

即对应的有3个，分别是；

对应的有2个，分别是；

所以函数的零点个数为5个。

例12.若函数有两个极值点，且，则关于的方程的不同实根个数是多少？

解 对函数求导可得，则极值点是的两个根。观察此方程与方程结构完全相同，

所以的两根为，，其中若，可判断出是极大值点，是极小值点。且，所以与有两个交点，而与有一个交点，共计3个。

若，可判断出是极小值点，是极大值点。，所以与有两个交点，而与有一个交点，共计3个。综上所述，关于的方程的不同实根个数共3个。

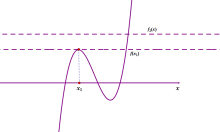
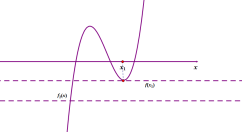
         图1                               图2

例13.已知函数，若方程恰有7个不相同的实数根，求实数的取值范围.

解 考虑利用图像变换作出的图像

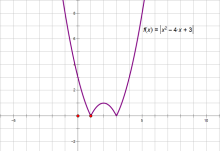
因为方程最多只能解出2个，若要出7个根，则，.

所以，

解得的取值范围为.

以上主要围绕定义域、值域或最值、导函数、单调性、零点等方面来介绍整体换元法在复合函数中的应用，但是复合函数的考查难度、深度、广度远远不止如此，又极具灵活性、多样性、创新性。由于笔者研究水平和时间所限，仍有许多问题有待进一步研究。在以后的教学实践中我会一如既往的继续努力，提升教育教学研究水平，持续探索教育理论，为实现国家教育现代化、建设教育强国贡献自己的力量。

参考文献：

[1]李京玉：高中数学解题思想方法之一       换元法，教育教学论坛，2017年12月第50期.

[2]张悦：中学数学中复合函数相关问题分析，中学数学研究，2019年第一期（下）45-49.

[3]侍昌亚：高中数学解题中换元法的运用，教学参谋，2016年9月.

[4]普通高中课程标准实验教科书必修部分，北京师范大学出版社，2011.