例谈平面向量数量积问题的复习策略 

例谈平面向量数量积问题的复习策略 

林雅彬

福建省莆田市擢英中学  351100

纵观近年来的高考试题，容易发现平面向量的数量积问题属于高频考点．由于这类问题时而需要从数的角度通过计算予以求解，时而需要从形的角度通过直观予以感知，解法多样、思维灵活，因而，平面向量的数量积问题一直都为高三复习所重视．本文将以笔者的教学实践为依托，谈谈如何把握平面向量数量积问题的核心内容，进而在有限的时间里，通过精讲精练，实现复习效果的最优化．

一、追本溯源，唤醒旧知

例1已知向量与的夹角为，且，，求的值．

解析：．

评注：通过本题复习向量的数量积公式和模长公式．以本例为基础，还可以编制如下变式题：

变式1：已知，，若与垂直，求向量与的夹角．

解析：依题可得，

故．又，所以，即与的夹角为．评注：通过本题复习了向量垂直的等价条件为两向量的数量积为0（前提：两个向量均为非零向量）再将数量积方式变形推出向量的夹角公式．

变式2：已知向量与的夹角为，且，，求与的夹角．

解法1（公式法）：

，

所以与的夹角为．

解法2（几何法）：

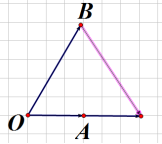
由向量的模长是模长的两倍，设，，即，故的几何意义为以的终点为起点，的终点为终点的向量，，，三个向量构成了一个等边三角形，易得所求夹角为．

评注：数形结合开阔了思路，诠释了向量的本质，通过形这座桥，直观得到问题的答案，同时还可很容易得到与的所成角．应强调，用图象法求角问题，需要将向量共起点后再得，否则会得错解．

变式4：若与共线，求．

解析：由向量共线得，即．

评注：本题复习了向量平行的等价条件及平面向量基本定理

变式5：已知向量与的夹角为，且，，求在上的投影．

解析：在方向上的投影为．

评注：要求向量的投影问题，可以由形的角度入手，这样无论向量怎么变化，解题路线只有一条．

变式6：中，，，求．

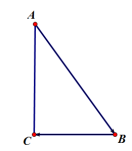
思路1（坐标法）：以C为原点，BC，CA所在直线为坐标轴，建系求解．

思路2（投影法）：由图形易得，在方向上的投影为．

思路3（基底法）：将用，表示，后使用公式法求解．

评注：本题看似常规，但解题的方法囊括了求数量积的三种常用方法，通过不同的视角解决数量积问题，有利于学生系统地认识问题．其中坐标法从代数的角度，投影法诠释了向量数量积的本质，将一个向量投影到另一个向量，要关注到投影向量的方向，这直接决定了符号的正负．基底法从向量的几何角度入手，将向量拆解成两个基底向量．一题多解，让学生清楚解决此类问题的常见方法，避免以后遇到此问题走弯路．在今后的解题受挫时，要想该问题考点是什么，之前同类型问题的解决方法是什么，往熟悉题靠拢，有了这数学意识，就可以给学生指明解题方向，构建及完善知识体系．

二、提升练习从定到动

例2已知是边长为4的等边三角形，为平面内一点，的最小值是（    ）．

A．B．C．D．

解析：以BC中点为坐标原点，建立如图所示的坐标系，

则，，，设，

所以，，，

即．

所以当，时，取得最小值．

评注：对于特殊三角形常用坐标法，假设动点的坐标，找出坐标满足的关系式，将问题转化为二次函数的最值问题，得解．

例3在中，，，，点是内的一点（含边界），若，求的取值范围．

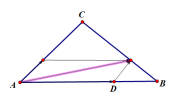解析：在线段AB上取点D，使，所以，

．由点是内的一点（含边界）可得，

．

所以，即．

评注：本题考查的是平面向量的模，考虑利用模长公式求解．

未知的只有，解决此题的关键就是求出的取值范围．结合极限思想和三点共线可得范围．

例4已知内接于圆，，，N是边BC上异于B，C的动点，求的取值范围．

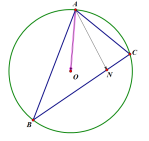解法1（基底法）：

，则，

整理可得，

，

又由垂径定理和向量数量积的几何意义可得，，．

因为，所以．

解法2（特例法）：

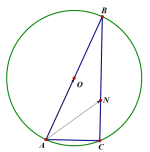由题目给定的条件，可以考虑用特殊三角形来求取值范围，将三角形看成以AB为斜边的直角三角形，以C为原点，，分别为轴和轴正方向，建系，也可求出取值范围．

评注：特例法是选择填空题中常见的解题方法，若找不到切入点时，可考虑让问题特殊化，正确率很高．

如何有效且高效地进行复习课教学是每位高三数学老师面临的重要挑战．从一类问题入手，说清该问题的常见解法，接下来让学生在实战过程中，有意识的对题目进行题型归纳，用课堂所归纳的解法进行解题．这样就使学生在学习时不停留于表面，而能透过题目考到题目的表征，系统地理解构建知识体系，最好掌握问题的本质，比较全面的看待数学问题．