忆本思源寻思路,拓展建模促提高

忆本思源寻思路，拓展建模促提高

毕传刚

安徽省安庆市太湖县实验中学 安徽省安庆市 246400

摘要 : 学以致用，是教师为学生传授知识的最终目的。要想学生能够灵活运用所学知识，教师在平时教学过程中，要通过例题、习题教学，引导学生进行知识、方法、数学思想等的总结。通过挑选典型习题的训练，让数学思想、解题方法得以强化，做到扎根于心里。这样，学生在遇到新问题时就会产生联想，建立起新旧问题的联系，把已有的思想方法迁移应用到解决新问题中。不仅能解决好新问题，而且能培养孩子创新思维能力、迁移应用能力。

关键词 : 学以致用 ，数学思想 ， 解决问题 ，迁移应用， 忆本思源

引 言：我校三月份中考模拟考试选用《安徽第一卷2022年安徽名校大联考试题》试题，其中第20题满分10分，智学网阅卷评分系统查阅我校1016人参加考试，得10分仅仅20人，人均得分1.98分，得分率很低。下面笔者从教材相关例题、习题内容与试题情境联系出发分析解题思路和解题方法，并对几何教学谈谈几点思考。

一、试题呈现：如图，△ABC内接于⊙O,AD⊥BC于D，BE⊥AC于E。

AD与BE相交于F。ON⊥AD于N,分别连接OA、OC。

1. 若∠AOC＝90°,求证：CD ＝DF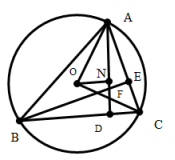

2. 求的值

二、试题分析

本题以圆内接三角形为问题背景，第一问证明两线段相等，所证线段分别是两直角三角形中的直角边，学生容易想到证△BDF≌△ADC。应用圆周角定理、三角形全等知识就能求证。第二问求线段ND与AF的比值，这里看不到常规的求线段比值问题的情境。常见的在有平行线条件或者有相似形条件下求线段比值学生容易解决，而本题已知条件中没有这些信息，学生又不能通过辅助线来创造条件，从而导致绝大多数学生束手无策，无从下手。阅卷系统数据显示第一问正确率为42.72%，而第二问正确率仅为1.97%。

三、忆本思源寻思路

好题用到的思想方法都能从课本中找到原型，在考题讲解中教师要能从问题的本源角度引导学生分析解题思路，寻找解题方法。

解法一：

思路分析：课本中例题、习题求线段之间比值关系，常常是通过找相似三角形或者平行线进行求解。观察线段ND、AF的位置，AF是△AEF的边，但ND不在三角形中，只需过O作OH⊥BC于H，即可将ND转移至OＨ，构造出△COH。根据圆周角定理和垂径定理，可寻找相似三角形并求出所求线段之比。

解答过程: 如图过O作OH⊥BC于H，连接OB，则四边形OHDN是矩形，所以OH＝ND，∵OB＝OC，OF⊥BC，∴∠COH＝∠BOC，CH＝BC 又∵∠BAC＝∠BOC，∴∠COH＝∠BAE。又∵∠CHO＝∠BEA＝90°，∴△COH∽△BEA，∴ ＝＝，∵BE⊥AC，AD⊥BC，∴∠CBE+∠ACB＝∠CAD＋∠ACB＝90°∴∠CBE＝∠CAD，又∵

∠CEB＝∠AEF＝90°∴△CEB∽△FEA，∴＝ ∴＝ 又∵＝

∴＝，∴OH＝AF，∵OH＝ND，∴＝。部分考生反馈也想到要构造直角△COH，但不能证出与△CHO相似的三角形。少数学生能够证出△COH∽△BAE，但是还是不能得出OH与AF的比值，只好做罢。这一证法要求学生能够熟练把图形与式子结合起来并进行转换，难在线段关系要通过两次三角形相似得出，并要进行多次转换。特别是＝的转换，学生难以想到。

解法二∶

思路分析∶根据已知分析图形特点，线段AF、ND在同一条线段AD上，且AF与ND有一段NF重叠在一起，联想到圆的轴对称性和线段大小关系比较中的叠合法，若沿着ON翻折，则线段ND就会叠合在NA上，点A落在下方半圆上，从而顺利找到第二种构造辅助线方法。

解答过程: 延长AD交⊙O于G，连接BG，∵AD⊥BC BE⊥AC ∴∠EBC＋∠ACB＝∠GAC＋∠ACB＝90° ∴∠GAC＝∠EBC 又∵∠GBC＝∠GAC ∴∠GBC＝∠EBC 又∵BD＝BD ∠GDB＝∠FDB ＝90° ∴△GBD≌△FBD ∴FD＝GD＝FG ON⊥AG ∴AN＝NG＝AG ∴AF＝AG－FG＝2NG－2DG＝2(NG－DG)＝2ND ∴＝。

这一解法源于课本圆的轴对称性、线段大小比较中的叠合法、三角形全等的运用。要求学生“见图思景”，具备良好的几何形象思维能力和勇于探索的创新精神。

解法三：

思路分析：MD与AF是在同一线段上且有重叠部分的两线段，直接求比值不容易求解。根据课本例题、习题解答经验可试着转移线段至另一位置，往往会收到“柳暗花明”的效果。根据AD⊥BC、BE⊥AC这一条件，通过构造直径对的圆周角和垂线，从而构造出平行四边形和矩形，顺利达到转移线段位置的目的。

解答过程：延长CO交⊙O于M，连接MA、MB。过O作OH⊥BC于H，∵CM是⊙O直径∴∠MAC＝∠MBC＝90° 又∵AD⊥BC BE⊥AC ∴BE∥MA BM∥AD ∴四边形AMBF是平行四边形 ∴AF＝BM，∵OH⊥BC ∠MBC＝90° ∴OH∥BM ∴△COH∽△CMB ∴

＝＝ ∴＝ ∵∠OHD＝∠HDN＝ ∠OND＝90° ∴四边形OHDN是矩形 ∴ND＝OH ∴ ＝。

这一解法通过构造直径和它对的圆周角、作垂线，从而构造出平行四边形和矩形，顺利将所求线段进行位置转移，从而构建出相似三角形，将所求线段之比转化为相似三角形对应边之比。创新思维得以展示，化归思想、建模思想得到很好应用。

四、教学思考

1.学以致用，学之能用，培养学生应用和创新能力是我们教学的最终目标。G·波利亚认为，解决一个问题之后，要善于去总结一个模型，并井然有序地储存起来，以后才可以随时支取它去解决类似的问题，进而提高自己的解题能力。① 教师在平时课堂教学过程中不能把得出问题答案作为最终目标。在问题解决后，要留出足够的时间让学生重温解题思路，总结解题方法，形成深刻认知。教师要引导学生总结常规解题方法，如本题中求线段比值用到的相似三角形法、转移线段法、叠合法等。对典型问题，教师要引导学生总结出数学模型，如“将军饮马模型”、“手拉手模型”，相似三角形中的“A字模型”、“8字型”、“一线三等角模型”等。当头脑中储存的方法、模型丰富后，遇到新问题时，才可能快速确定思考方向，形成简洁的直觉形象思维，创造性地解决问题，提高解决问题的能力。

2.教师要激发学生的探究热情，鼓励孩子敢于突破思维局限，大胆探究。如老师可借助数学应用题教学，启发学生构建不同的等量关系，列出不同的方程求解。利用几何证明题教学，引导学生能“执因索果”，又能“执果索因”，提高学生分析、解决问题的能力。启发学生从不同角度思考问题，引导学生思考能否一题多解。教师可通过评选“解题小能手”活动，激发学生探究问题的内驱力。通过一题多解的教学，训练学生的发散思维和创新思维，提高学生分析与解决问题的能力。

参考文献①赵雄辉、刘云章，怎样教解题————波利亚数学教育思想研究选讲[M],长沙:湖南教育出版社，2015

1