数学解题中的认知结构构建下的数学联结

数学解题中的认知结构构建下的数学联结

1 吴焕平 2 刘国华

1 西藏山南市曲松县中学湖北省援藏教师 856304

2湖北省武汉市关山中学 430000

【摘要】学习是一种认知的联结，联结是从尝试错误刺激反应的发展到有意义的学习。数学学习实际上是寻求“元认知的构建”， 构建数学认知结构的过程。以数学知识结构为基础，以学生原有不同的数学认知结构为出发点，以学生发展为目标达到构建学生的认知结构，作为促进学生有意义的联结的导向策略。

【关键词】认知的联结 认知结构 导向策略

一、引言（数学新课标的解读）

全日制义务教育新《数学课程标准》明确指出：“有效的数学学习活动不能单纯地依赖模仿与记忆”，教师应当帮助学生“在自主探索和合作交流的过程中真正理解和掌握数学知识与技能、数学思想和方法，获得广泛的数学活动经验”。这实际上从一个角度要求数学教师，要重视学生的元认知学习。但在实际教学中，学生的学习似乎还停留在“S—R”阶段。这种简单的操作方法在短时间内能使考试成绩上去，但代价是使学生背负沉重的学习负担，并造成学生思维僵化，不利于培养“创新型”人才，与素质教育背道而驰。本文就数学学习的元认知联结问题及导向策略上作一些探索。

二、关于联结理论

学习的联结理论强调复杂行为是建立在条件联系上的复合反应，学习就是在刺激与反应之间建立联结的过程。联结论又称刺激（S）—反应（R）学习理论，是由“教育心理学鼻祖”—美国心理学家桑代克创立。联结论对学习心理问题提出了非常有价值的见解，许多理论至今仍在指导教育、学习实践活动，但其根本缺陷就是忽视了对学习的内在心理过程的深入分析。

而认知理论（theories of cognition）是关于有机体学习的内部加工过程，如信息、知识及经验的获得和记忆、达到顿悟、使观念和概念相互联系以及问题解决的各种心理学理论。持学习的认知观的理论家有德国格式塔学派的主要代表人物、瑞士的皮亚杰、美国的布鲁纳与奥苏伯尔。尽管他们彼此间存在很大差别，但在学习问题的观点上有一些共同特点。一是他们确认，有机体习得的是知觉或认知结构的形成与变化。即学习的基础是有机体内部的、有组织的结构的形成与改组，而不是刺激（S）与反应联结(R)的形成或行为习惯的加强或改变。二是他们相信，影响学习的主要变量（O）是刺激情境的整体性、突然的理解或知觉、有意义的发现与接受、认知结构的特点、注意或心向，而不是刺激与反应的接近、强化、强化程式。这一理论与发展智力和培养创造能力的教育理论相符，对解释较高级的认知学习较适合。

但时至今日，在数学教育中，我们不能不重视，数学学习重要的应该是认知学习，它是一个建立学生心理内部学习机制的过程。这里要明白三点：（一）要利用学生原有的认知结构，（二）要重视学生一定年龄阶段的心理发展水平，（三）要充分考虑不直接参与的情感、意志、兴趣等问题。

三、数学习题解答的两种联结思想剖析

下面结合教学实践，说明“S—R”与认知结构联结之间的各自意义。

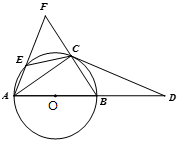例题、如图，AB是⊙O的直径，点D在AB的延长线上，

C、E是⊙O上的两点，CE=CB,∠BCD=∠CAE，

延长AE、BC相交于点F;

求证：（1）CD是⊙O的切线；（2）求证：CE=CF.

按“S—R”的行为主义联结理论，可以让学生直接操作，学生可能不去仔细审题。由图形“先入为主”，不断尝试，不断碰壁，然后再回头去审题。在点、线、角、三角形、圆的离散图形中不断产生错误。偶尔碰上解题思路，才得到问题的解决。之后，再不去认识、总结。下次在碰上此题，又重新错误尝试。

下面我们在认知结构构建下的数学联结对本题进行解答：

通过上面的解答及对比认知结构构建下的知识联结的分析，使学生在原有的认知结构思维水平基础上发展他的联想思维，使新旧知识加以联结，找到证题方法，达到解决问题，建立起新的认知结构。

因此，我们在教学中，一定要把精力花在建立学生认知结构上。少用或不用“S—R”这种“尝试错误”的机械方法，多用科学成功的尝试，引导学生认真寻求“中间变量”，努力使学生的新旧知识加以联结，促进学生的数学素养不断提高。

事实上就学习者对数学问题的解决，无论是数学概念的形成、数学技能的掌握，还是数学能力的培养，都是学习者由未知到已知的联结过程，即“S—R”的联结过程，重要的是寻求“中间变量O”，从而构建数学认知结构。所谓数学认知结构，就是学生通过自己主动的认识而在头脑里建立起来的数学知识结构。

教师在对于这样的问题解答和分析过程中，一定要对于题设条件与结论之间存在的知识构建，知识元之间的联结作出分析，这需要老师以数学知识结构为基础，构建学生的数学认知结构，学习过程就其本质而言是一种认识活动。因此，数学教学的根本任务是发展学生的数学认知结构的构建。

在对于问题解答完成后老师要组织学生，分析数学知识的整体联系、注意揭示数学思维过程、有机渗透数学思想方法。所谓数学思想方法就是数学活动的基本观点，它包括数学思想和数学方法。数学思想是教学思维的“软件”，是数学知识发生过程的提炼、抽象、概括和提升，是对数学规律更一般的认识，它蕴藏在数学知识之中，需要教师引导学生去挖掘。而挖掘的过程就是数学认知结构形成的过程，也就是数学学习的最佳联结过程。数学方法是数学思维的“硬件”，它们是数学知识不可分割的两部分。