高中立体几何动态变化问题教学实践

高中立体几何动态变化问题教学实践

张晶

浙江省舟山市白泉高级中学 浙江省舟山市 316000

摘要：在高中数学教学中，立体几何动态问题是教学的难点、高考的热点，问题中的“不确定性”与“动感性”元素往往成为高中生思考和求解问题的思维障碍，导致解题过程不够顺利、试题得分不尽如人意。

关键词：高中；立体几何；动态变化；教学实践

实际上，立体几何动态问题在变化中总会蕴含着某些不变因素，我们唯有认真分析其变化特点，找到其中不变的静态因素，从中发现和寻找解决问题的突破口。在动态问题求解过程中，教师要引导学生进行积极思考，借助动态思维来观察变化规律，或者把动态转变为静态，从而正确求解问题答案。

一、立体几何动态变化问题教学困境

在立体结合动态变化问题教学中，课堂教学往往面临以下困境：（1）教学中采取“满堂灌”方式，不利于学生学会、弄懂，降低了课堂探究质量和效率；（2）无法发挥学习主体作用，课堂讲解得多、讲的速度快，不给思考空间和时间，讲评式教学降低了学生参与课堂积极性，容易失去学习兴趣；（3）课后反思和总结不足，很多学生课堂感觉听懂，但课后练习依然存在问题，缺乏课后反思和总结能力，课后反思和总结不足遇到类似问题依然不会、不懂。

二、立体几何动态变化问题分类解题策略

1.角度问题

角度问题是立体几何动态问题中重点试题之一，注重考察学生对角度求解，锻炼学生数学思维能力。数学教学中，教师要关注学生学习情况，引导他们对问题进行深入讨论，寻找到该类问题的通用解法。在思考过程中，高中生要探讨和寻找最值条件，发现角度变化规律，依据规律来求取问题答案，发展数学思维能力。

如图1所示，四边形ABCD和ADPQ均为正方形，所在平面相互垂直，已知动点M在线段PQ上运动，E、F分别为AB、BC的中点，假设异面直线EM与AF所成夹角为θ，则cosθ的最大值为_____。作为立体几何动态问题中一类重要题型，求解空间角度一般有两种方法：（1）寻找到某个点来建立空间直角坐标系，借助于坐标系内点坐标来运用公式进行求解，通过代数法来解答得到问题答案；（2）分析题目中图形，结合图形来求取最大（小）值。借助于该问题，教师引导学生以小组为单位进行思考，寻找求解方法，学生发现：当点M位于P处时，EM和AF所成角为直角，此时余弦值为0（最小）。当M点向左移动时，EM和AF所成角逐渐变小，点M与Q点重合时角最小，余弦值最大，计算后求得答案为2/5。

图1

2.距离问题

与角度问题类似，距离问题也是高中立体几何问题研究的重点，求解方法与角度问题有着相似之处，教师在教学中不妨把两种试题混在一起来考察学生应用知识能力。数学教学中，教师要关注班级实际学情，关心班级每个学生的学习情况，帮助他们树立好学好数学知识信心。

在学习完数学立体几何角度知识后，教师要重视试题讲解过程，引导学生进行试题训练，对知识进行梳理，提取其中的数学知识，注重求解角度思路的迁移与发展，扩大数学知识应用范围到距离方面。实际上，高中生在新知识学习中要构建认知结构，以角度和距离的试题练习来促进对所学知识理解和掌握，扩大知识认知范围，在试题讲解中渗透知识迁移过程，发展数学解题能力。由此可知，高中数学立体几何动态试题讲解中要注重渗透知识迁移过程，发展学生概括总结能力，培养知识迁移能力。

3.面积、体积问题

面积、体积类问题较角度和线段难度变大，求解方法多种多样，要求高中生要具备灵活应用知识能力，破解遇到的难题。在求解面积、体积类问题时，学生要寻找解题规律，从熟悉思路出发来求解，注重思维发散性，遇到困难及时转换思路，提升解答正确率。

如图2所示，棱长为2的正方体ABCD-A₁B₁C₁D₁中，M是棱AA₁中点，点P在侧面ABB₁A₁内，若D₁P⊥CM，则△PBC面积最小值为_____。本题是以学生常见的正方体作为载体，已知线线间垂直，再结合立体几何中的动点问题来确定三角形最值。在本题中，命题人注重考察学生的应用知识能力，解法多种多样，有利于区分学生层次。解法主要有以下几种：（1）分析何时PB最短，运用等积法思维来求解线段PB最短距离，进而求出最小面积；（2）利用向量法来确定线段PB最短距离来求解最小面积；（3）建立空间直角坐标系来根据条件求出对于向量积为0时确定三角形面积。结合上述三种求解方式，我们发现最小面积求解思路多，学生要具备灵活运用知识能力，教师课堂多留出时间供他们进行思考，在思考中发展数学思维，形成解答几何动点问题能力。

图2

4.轨迹问题

在很多学生看来，轨迹问题是学习中难度最大的一类问题，高中数学教师要重视轨迹问题的讲解，引导学生由浅入深、步步深入地求解轨迹，形成数学思维。求解轨迹问题时，要能够熟练运用所学知识来进行求解，结合已有解题思路来探索，从中发现轨迹变化，形成正确解题思路。在解答轨迹问题时，教师要引导学生思路回归到几何图形的有关轨迹定义上，探讨运动轨迹是否符合某个已有图形的定义，采取“以静制动”教学策略来求解动点问题。

如图3所示，AB为平面α上的斜线段，其中，A为斜足，若点P在平面内运动来使得△ABP面积为定值，那么动点P的轨迹是_____。认真分析本题，发现本题动点P有两个条件：（1）平面内运动；（2）△ABP面积为定值。根据三角形定义，边AB长度一定，要想确保△ABP面积为定值，那么，点P到线段AB距离必定为定值，因此，点P轨迹为以直线AB为旋转轴的圆柱面（图4所示）。再结合条件（1），根据圆锥曲线中椭圆定义，我们发现点P的轨迹是椭圆。通过上述试题，教师要引导学生对问题进行思考，解题过程中注意轨迹与已知曲线关系，从中找到二者间联系，发展数学核心素养和综合能力。

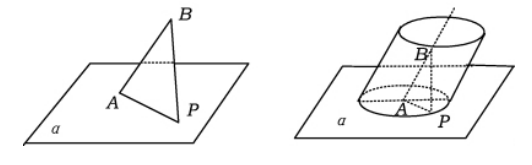
图3 图4

总之，立体几何动态问题是高中数学教学中的难点，教师在授课时要关注实际学情，从多个角度引导学生对知识进行探究和思考，“以静制动”来探究动与静间关系，有效促进个体数学学习质量和效率，使每个人都能从中发现、找到解题思路，发散数学思维来形成创新意识，发展立体几何解题综合能力。

参考文献：

[1]李健.例析立体几何中的动态问题[J].中学数学,2012(21):26-27.