浅析分式方程增根的溯源及应用

浅析分式方程增根的溯源及应用

张美玲

陕西省汉中市汉中东辰外国语学校 陕西汉中 723000

【摘 要】分式方程是初中数学学习的一个重要内容，同学们在学习这部分内容时，常常对分式方程的增根及其产生原因理解不清，造成在解决有关问题时出现这样或者那样的错误，解分式方程应须研究增根问题，本文对分式方程产生增根的原因进行分析,进而归纳出解决这类问题的一般形式，并把它作为解分式方程的理论依据。
【关键词】 分式方程 增根 去分母

方程分为整式方程和分式方程，其中分母含有未知变量的方程就叫分式方程。会解分式方程是初中数学中的重点也是难点，更是初中数学命题的热点。如果将分式方程的增根问题解决好了，将会大大增加解题的正确率，减少不必要的错误和遗憾。分式方程增根问题，是分式方程教学的一个难点，许多学生学后也是似懂非懂。老师在讲这一课时，同样感到很吃力。因此在教学实践中，需要重视研究分式方程的增根。教学中在解分式方程时，通常先把分式方程去分母，转化为整式方程，由于去分母扩大了变量的取值范围，在所解得的根中使分母为零的根就是该分式方程的增根，所以验根是解分式方程中必不可少的环节。那么好多同学非常疑惑：解分式方程为什么需要验根呢？增根是如何产生的？增根是分式方程所特有的吗？

一、要弄明白这个问题，我们必须要弄明白以下几个问题

首先，我们需要明确什么是分式方程的增根？

分式方程的增根,并不是指在解分式方程的过程中出现错误而得到的根,而是在将分式方程化为整式方程后求得的未知数的值。如果使分式方程的最简公分母的值为0 ,那么这个根是分式方程的增根。我们要判断解得的未知数的值是不是原方程的增根,只要将其代入分式方程的最简公分母中去计算就行了。若最简公分母为0 ,则这个根是原方程的增根,若不为0 ,则这个根就是原方程的根。

其次，我们需要弄清楚分式方程产生增根的原因是什么？

分式方程增根产生的原因我们可从以下三方面理解: 一方面， 根据同解原理:等式两边同乘以(或除以) 一个不为零的数或代数式,所得的方程与原方程同解,解分式方程时,在将分式方程转化为整式方程的过程式中,由于在方程两边同时乘的是一个代数式 ,而这个代数式的值为不为0 ,是由其中所含的未知数的值来确定的。当我们解出的未知数的值使这个代数式为0的时候,就相当于在方程的两边同时乘的是一个0 ,所得方程与原方程不同解,因而这个未知数的值当然不是原来方程的根。第二方面，在将分式方程转化为整式方程的过程式中,方程中未知数的取值范围扩大而造成的。第三方面，这个无解的分式方程原来本质上是一个矛盾方程，由于我们在去分母的过程中，在矛盾方程的两边同乘以0，使得原本矛盾的方程变成了0=0，也就不矛盾了，所以增根是变形后的整式方程的解，而不是原分式方程的解。

例如解分式方程 =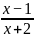

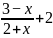
方程中未知数的取值范围是x≠-2，但通过去分母化为整式方程x-1 =3-x+2（2+x），整理得0=8,未知数的取值范围扩大为全体实数了, 解整式方程x-1 =3-x+2（2+x）得到的解x不在原方程取值范围内,因此它不是原方程的根，此方式方程无解。

最后我们再来了解分式方程的增根与分式方程无解有什么内在的联系？

虽然分式方程有增根,但不一定无解；反之，分式方程无解,也不一定有增根,但两者,是解分式方程中的常客,常常结伴而行。分式方程无解有两种情形: 一是分式方程式化成整式方程后, 这个整式方程本身就无解,此时的分式方程是无解的,也不存在增根。二是分式方程化成的整式方程有解,但这个解是分式方程的增根,此时分式方程也无解。因此我们在考虑分式方程无解的时候,一定要考虑到增根的情况。

二、分式方程的增根在解题中的注意事项

分式方程的增根虽常常令同学们吃亏不小,但只要我们能正确认识,摸清增根本质,增根就会为我们服务的。在解分式方程的过程中，分式方程的转化为整式方程（去分母）时, 方程两边同时乘以的最简公分母，未知数的范围扩大了，就会产生增根，增根必须同时满足两个条件, 分式方程的增根能使分式方程转化成的整式方程时，方程两边同时乘以的最简公分母等于0，分式方程的增根能使分式方程转化成的整式方程成立。我们要清醒的认识到：增根一定能使最简公分母等于0，反过来，能使最简公分母等于0的未知数的值却不一定是分式方程的增根，其次，不是每一个分式方程都有增根。解分式方程常见的3个误区，下面举例说明:

误区一：认为能使分式方程转化为整式方程时，方程两边同时乘以的最简公分母等于0 的未知数的值，都是分式方程的增根。

例如在教学人教版9.7节分式方程第二课时，有一道探索性题，解方程 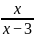= 2 — 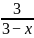求它的增根。

解：因为方程有增根，所以令x-3=0，得到x=3，因此方程的增根是x=3。点评：本题的解法是正确的，这个分式方程转化为整式方程是x=2（x-3）+3，解x=3同时满足增根的两个条件。

例：解分式方程 + =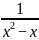

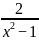
方程的最简公分母是x（x+1）（x-1），若x（x+1）（x-1）=0，则x=0或1或-1，这3个值显然不都是增根。转化成的整式方程的解x=1，因此，只有x=1是增根，另外2个值不符合前面提到的增根的必须条件的第二个条件。点评：一定要注意增根所必须同时满足的两个条件。

误区二：认为分式方程的增根和分式方程无解是等同的。这是错误的,当分式方程无解时,分式方程可能有增根;还有另外一种可能,分式方程转化成的整式方程如果没有解,那么分式方程也是无解的。出现这种错误的原因是常见这样一类题目，举例如下：

例：解分式方程 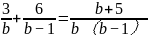①

方程两边都除以b（b-1），得3（b-1）+6b=b+5 ②，解这个方程，得b=1.经检验：当b=1时，原方程无意义，，所以b=1是原方程的增根。所以原方程无解。

分析：显然方程①中未知数b的取值范围为b≠0且b≠1，在去分母化为方程②后，未知数b的取值范围扩大为全体实数，所以当求得的b值恰好是最简公分母为0时，b的值就是增根。本题中方程②的解b=1，恰好使公分母为零，所以b=1是原方程的增根，原方程无解。

误区三：忽视增根的存在

例如：已知关于x的方程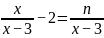 有一个正数解，求n的取值范围。（错解）去分母得x-2（x-3）=n，所以x=6 - n，由题意知X >0,所以6 - n > 0，得到n<6.

错解分析：忽视了分式方程有可能产生增根的情况，即还需满足x≠3，即6- n≠3，n≠3。正确答案： n<6且n≠3。

综上所述，对于分式方程一定要明确增根，同时必须验根。

总结:通过以上3个例子可知，解答此类问题的基本思路是:把所给的分式方程转化为整式;根据所给方程确定增根;把增根代入整式方程,求出字母数值。

分式方程的增根使数学问题摇曳多姿、妙趣横生，在执著追求数学真谛的历程中，问题是数学的心脏,探究性的问题始终是推动探索数学世界的动力源泉，能够有效地激发人的积极性,引发数学思考,推动创造性思维的产生.以上对增根无解及有解的类型做了简要梳理和归纳,同时编写了几个对应的分式方程.由此沟通了分式方程与分式的纵向联系,渗透了具体到抽象,经历了特殊到一般再到特殊的整体思想, 关于分式方程增根问题,在现行人教新课标课本上提及不多，但作为教学一线的数学教师，有必要引领学生加以探索和总结，对学生更好的探究学习数学知识具有现实指导意义。

参考文献：

[1]杨裕钱,董林伟.义务教育数学教科书[M].南京:江苏科学技术出版杜,2012.

[2]教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.