初中数学常见“几何最值问题”探析

初中数学常见“几何最值问题”探析

黄哲

广西合浦县山口镇初级中学 536122

摘要：初中阶段的几何动态问题中，在一个几何元素给出条件变动时，求长度、面积和周长等几何量的最大或最小值，称为最值问题。我国各地中考数学几何题重点考察学生空间想象能力、实践操作能力和解决问题能力等，本文将结合实际情况对几何最值问题进行简要分析。

关键词：初中数学；几何；最值；解决方法

引言

新课程改革以来，数学教育越发受到关注，数学文化在教育中处于领先地位。数学文化对数学教育具有积极作用，为积极响应我国课程标准，应将数学文化融于初中数学课程。笔者将初中几何课程作为研究对象，通过教育教学各个环节，对所开发成果进行改进与完善。

一、应用几何性质

（一）利用两点之间线段最短原理解题

图1为一个圆柱体，其半径为4厘米，高为18π厘米。圆柱两个底面的圆周上点A和点B，并且这两点在同一母线上，用一条线围着圆柱侧面绕三圈刚好可以从点A到点B，请求出这条线的最短长度是多少。

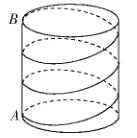
图1

分析：将圆柱展开成一个长方形，如图2，这条线最短长度是三条斜线的长度总和。第一条直线与底面圆的周长，以及圆柱三分之一的高形成一个直角三角形。

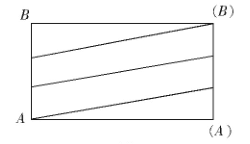
图2

根据周长公式可知，底面圆周长为8π厘米，圆柱高的三分之一为6π厘米。根据勾股定理，可得一条斜线长度为10π厘米，因为三条斜线组成的是平行四边形，所以斜线长度相等，所以，这条线长度最短为30π厘米。两点之间，线段最短使初中学生需要掌握的基本内容之一，人们在日常生活中也在不断验证。初中数学教学过程中，短距离问题是重要知识，更是中考热点题型。近些年，经常出现“最短类”题型。根据这题可知，最值问题与立体图形相结合的题型，往往需将立体图形转化为平面图形，也就是绘制出立体图形的展开图，进而利用“两点之间，线段最短”原理，结合勾股定理，进行解题。这些原理在整个初中阶段有着非常广泛的应用。初中数学教师应在总复习时，将这类问题进行整合，分类讲解，可以使学生更好的运用。

（二）利用三角形三边关系解题

在图3中，∠MON = 90°，矩形 ABCD的顶点A在边OM上，顶点B在ON上。在矩形 ABCD的形状保持不变的前提下，A在OM上的运动随着B在ON上的运动而变化，AB = 2，BC = 1，运动过程中，点 D 到点 O 的最大距离是多少。

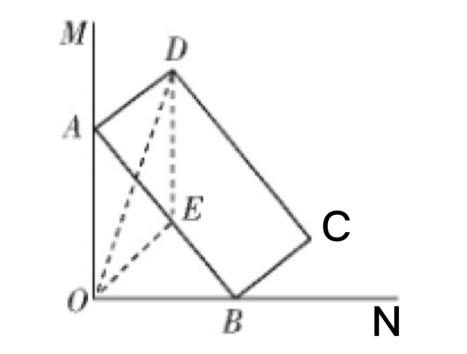
图3

分析：在图3中，取 AB 的中点 E，连接 OE、DE和OD。因为 OD ≤ OE + DE，所以当 O、D、E 三点共线时，点 D 到点 O 的距离最大，此时，AB = 2，BC = 1，所以 OE = AE =1/2AB = 1。所以 OD 的最大值为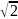 + 1。由此题可知，这种题型往往需要结合实际图形的特征，并利用其图形特征，将问题转化到三角形三边关系相关原理，从而解决问题。在学生初步认识三角形三边关系后，这部分知识内容可以帮助初中生对周围事物加深理解，更可以利用此内容解决问题。在授课过程中，教师应多多提供给学生自己动手操作的机会，方可使学生充分掌握三角形三边关系的特性。比如，教师可以利用生活中积累的经验，为学生创设有效的实践活动，使学生在实践中，感悟其中原理。当学生发现三角形中，两边之和大于第三边的规律，可以让学生进行探究反思。所谓动点问题，即图形中存在可以运动的点，在线段上运动的题目。这类题型解决的有效方法是动中取静，使动点定下来，在通过相关知识定理解题。动点问题的解题思路为：在变化中找到不变的性质。

（三）利用垂线最短解题

在图4中，A点的坐标为( －1，0)，点B在直线 y = x 上运动，当线段 AB 最短时，点 B

的坐标为（ ）

（A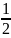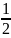）（- - ，- - ）（B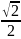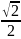）（ ， ）（C）（0,0）（D）（- ，- ）

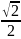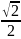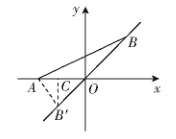
图4

分析：因为点 B 在直线 y = x 上运动，所以△AOB' 是等腰直角三角形，所以△B'CO 为等腰直角三角形。因为点 A 的坐标为（－ 1，0），所以OC = CB' =1/2OA=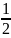 ，所以点B的坐标为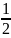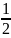（- - ，- - ），因此选择选项A

（四）利用轴对称解题

在图5中，有正方形ABCD，BC = 8,BC 的中点为点E,点对角线 AC 上有一个动点P，求

BP+ EP的最小值是多少。

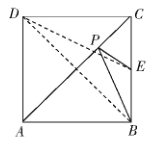
图5

分析：连接DE，交BD于点P，连接BD。因为点 B 与点 D 关于 AC 对称，所以DE 的长就是BP+ EP的最小值。因为点E是BC的中点，BC=8。所以CE = 4。在直角三角形CDE中，DE = 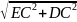=5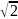 。本题的难点在于需要画辅助线，在这种题型中，可以通过图形规律画出辅助线。在讲解此种类型题时，教师可以引导学生进行画线，从而培养学生数形结合的思维，使学生再次遇到这种题型时，可以及时形成解题思路。中考数学压轴题渐渐转向动态几何和实验探究题型。学生对几何图形的运动变化考核更加严格，在解题过程中，学生可以通过翻着图形、对称图形等方法，研究图形的变化以及图形性质。学生在经历了自主探究后，可以将运动观点和转换思想结合起来，提高其逻辑思维能力、分析能力等。

二、代数证法

（一）利用一元二次方程根的判别式

已知:x＞0，y＞0 且-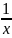 +- 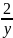= 1，求 2x + y的最小值。

分析：使2x + y = t，可得y = t－2x。将其带入-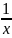 +- 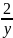= 1中，得出- 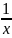+- 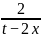= 1，2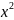 －tx + t = 0。因为x 是实数，所以Δ = t 2－8t≥0，所以t≥8，或 t≤0。又因为x＞0，y＞ 0，

可得t≥8．

故 2x + y 的最小值为8。

（二）利用配方法进行解题

图6是一扇窗户，窗户由半圆与矩形组合而成。已知窗户周长是8米，在保证窗户透光性最好的前提下，怎样求出最大面积？

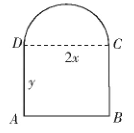
图6

分析：可以用x 表示半圆半径，y表示矩形边长AD，可得2x + 2y +πx = 8，所以，y =-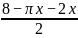 。设窗户的最大面积为 S，则S = 2xy + 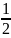π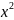 ，两个式子结合，y =- 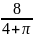=x,也就是说，窗户周长固定时，其下部长方形的宽正好为半径时，窗户面积最大。初中数学竞赛中常常出现一元二次方程的整数根的题型。这类问题涵盖知识面比较广泛，包括方程相关内容和整数相关内容。其中的数学思想受到很多命题人员的喜爱。然而，部分学生在进行解题时，没有解题结构，缺乏思考方法。甚至有小部分学生对题目无从下手，这就需要数学教师进行分类讲解。这这种题型中，计算量相对较大，教师需要引导学生耐心对待。这类方程相关的题型，可以锻炼学生的思维能力，使初中生的思维更加灵活敏捷。解题时要分析其特征，运用初中所学数学知识，选择相对简单的解题方法。这种题型所占比重很大，学生有必要提高解题思路，锻炼解题能力。公式法、配方法和因式分解法是解一元二次方程的常用方法，所以，初中数学授课过程中，要加强对这几种方法的练习。

三、结束语

总之，初中数学教学中，几何最值问题的教学一直是一个难题。部分学生对此没有清晰解题思路，教师应根据学生实际学习情况以及个体差异，通过有效教学手段讲解几何最值问题的解题思路，并进行相关题型练习，提高学生解题能力。

参考文献：

[1]吴世平. CAMI在初中几何教学的应用研究[D].湖南科技大学,2015.

[2]马心雨. 数学文化视角下初中几何教学设计研究[D].辽宁师范大学,2020.

[3]蒋雁. 基于核心素养背景下初中几何最值问题的解题方法[J]. 数理化解题研究,2019(20):33-34.

[4]兰春燕. 初中数学常见“几何最值问题”探析[J]. 福建基础教育研究,2019(08):65-67.