探寻“解”的奥秘

探寻“解”的奥秘

兰芳

山东省滨州市滨城区梁才街道办事处中心学校 山东 滨州 256600

我们经常会遇到这样一类题目，某方程无解，求字母系数的值；或某方程组有两组不同的解，求字母系数的取值范围。对于这类题目，学生们往往觉得无从下手，不知道题目的已知条件在告诉我们什么，应该根据什么去寻找解题思路和方法。出现这种情况的原因主要是学生对于方程和方程组的解的情况由什么来决定，掌握的不好，只要找到了决定方程和方程组的解的情况的根源，问题就迎刃而解了。基于这种情况，我现将在初中阶段学过的几类方程及方程组解的情况作一下归纳和总结。希望对学生们解此类题型会有所帮助。

在初中学过的方程及方程组主要有：一元一次方程、一元二次方程、二元一次方程组、二元二次方程组、分式方程等。一元二次方程解的情况，课本上有详细的讲解说明，在这里我就不再多说。在这里我主要介绍一下其它几类方程和方程组的解的情况。

一、一元一次方程

在分析一元一次方程的解之前，要先对方程的解的概念明确理解。“使方程左右两边相等的未知数的值，叫方程的解。”所有的一元一次方程最后都能化成最简形式ax=b。①当a≠0时，根据方程同解原理，可得方程的唯一解x=;② 当a=0，b≠0时，任何实数都不会使方程两边相等，由方程解的定义可知当a=0，b≠0时，方程无实数解；③ 当a=0，b=0时，把任何实数代入方程都会让方程两边相等，根据方程解的定义可知，所有的实数都是它的解，即当a=0，b=0时，方程有无穷多个解。知道了一元一次方程解的情况，就可以据此来解题了。例如

例1、已知关于x的方程a（x-3）+b（3x+1）=5x+1有无穷多个解，求a、b的值。

分析：这是一个关于x的一元一次方程，由它有无穷多个解，可知将这个方程

整理成最简形式后，未知数的系数和常数项都为0，这样就可以得到两个关于a、b的方程，解由这两个方程组成的方程组就可以求得a、b的值。

解：原方程可整理为（a+3b-5）x=3a-b+1因为原方程有无穷多个解，所以

解得a= ,b=

二、二元一次方程组

解二元一次方程组的基本思路是消元转化为一元一次方程来解，因此，二元一

次方程组解的情况要由消元后所得的一元一次方程来决定。对于已知二元一次方程组解的情况，求字母系数的值及取值范围的题目的做法应该是：把二元一次方程组消元化为一元一次方程，根据已知条件可得这个一元一次方程解的情况，从而求得字母系数的值及取值范围。

2. 关于x、y的方程组

无解，求m的值。

解：①×2+②得4x+mx=5

整理，得（4+m）x=5

因为原方程组无解，所以方程（4+m）x=5无解

即4+m=0 得m= - 4

三、二元二次方程组

二元二次方程组的解题思路是消元化为一元方程或降次化为二元一次方程组来

解。那么二元二次方程组的解的情况就由由二元二次方程组转化得到的一元方程或二元一次方程组来决定。即根据题目条件我们就可以得到由原方程组经过消元或降次所得的方程或方程组有怎样的解。

例3、m为何值时，方程组

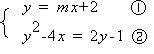
⑴有两组实数解；⑵有一组实数解；⑶无实数解。

解：把①代入②得（mx+2）² - 4x=2(mx+2)-1

整理，得m²x²+(2m-4)x+1=0

⑴因为原方程组有两组实数解，所以m²x²+(2m-4)x+1=0

是一元二次方程，且有两个不相等的实数根，即

解得m<1且m≠0

所以，当m<1且m≠0时，原方程组有两组实数解。

⑵由原方程组有一组实数解，可得两种情况：

①当m²≠0时，此方程为一元二次方程，有两个相等的实数解，即

Δ= -16m+16=0 解得 m=1

②当m²=0时，即m=0时，方程m²x²+(2m-4)x+1=0

是一元一次方程，只有一个解，故此时原方程组有一组实数解；

∴当m=1或0时，原方程组有一组实数解。

⑶因为原方程组无实数解，所以方程m²x²+(2m-4)x+1=0无解，即

解得 m>1

所以，当m>1时，原方程组无实数解。

例4、已知方程组

有两组实数解，求a的值。

分析：既然条件与方程组的解有关，那就先来看一下如何解这个方程组。由方

程组的特点可把原方程组化为两个方程组 和 因为原方程组有两组实数解，那么这两个方程组解有两

种可能：第一、这两个方程组分别各有一组解；第二、这两个方程组中有一个方程组有两组解，另一个方程组无解。到底是哪一种情况呢？根据上面的知识我们知道这两个方程组的解有几个，要由这两个方程组消元后所得的一元方程来决定。因此，可先把这两个方程组消元化为一元方程再来判断它们解的情况。

解：原方程组可化为两个方程组

（I） 和（II）

方程组（I）消元可得方程⑴2y²+2ay+a²-1=0

方程组（II）消元可得方程⑵2y

²-2ay+a²-1=0

方程（1）的判别式△₁=(2a)²-4×2(a²-1)=4a²-8a²+8=8-4a²

方程（2）的判别式△₂=(-2a)²-4×2(a²-1)=4a²-8a²+8=8-4a²

可见这两个方程的判别式相等，即这两个方程解的情况是相同的，因为原方程

组有两组实数解，所以，这两个方程分别各有一个解（即各有两个相等的实数解）。所以8-4a²=0,解得a=±

所以，当a=±时，原方程组有两组实数解。

另注：若例4中的原二元二次方程组化成了几个二元一次方程组，那a的

确定方法同上面二元一次方程组中字母系数的求法。

四、分式方程

因为分式方程的解题思路是把分式方程化为整式方程，因此，分式方程的

解可以利用它所化成的整式方程来判断。又因为在把分式方程化为整式方程的变形过程中可能会使原分式方程产生增根，因此，分式方程的解并不能完全由它所化成的整式方程来决定，还要考虑增根的可能。例如

例5、关于x的方程 = +2无解，求m的值。

分析：此方程无解的可能有两个：①它所化成的整式方程无解；②它所化成的

整式方程有解，但这个解是原分式方程的增根。

解：原方程可化为x-1= m +2（x-2），整理，得x=3-m

很显然，这个整式方程有唯一解，但是原分式方程无解，所以x=3-m是原方程

的增根

即x=3-m=2 所以m=1

例6、已知方程- =1+无实数解，求实数m的取值范围。

解：原方程可化为x²-x+2-m=0,此方程为一元二次方程，因为原分式方程无实

数解，所以有两种情况：

①方程x²-x+2-m=0无实数根，即△=（-1）²-4(2-m)=1-8+4m=4m-7﹤0,∴m﹤，

所以当m﹤原分式方程无实数解。

②方程x²-x+2-m=0的解是原分式方程的增根，即此整式方程的根是x=1或0，把x=0代入x²-x+2-m=0得m=2;当m=2时，方程为x²-x=0,此方程解为x₁=0,x₂=1。x₁=0,x₂=1都是原分式方程的增根，所以，当m=2时原分式方程无实数解；

综上所述，实数m的取值范围是m﹤或m=2。

很显然，对于已知方程或方程组解的情况，求字母系数的值或取值范围，这类

题并不难。关键是了解是什么决定了方程或方程组有解，有什么样的解或者是无解。即知道通过已知条件我们能得到什么，找到了问题的根源，知道了解题的思路，那问题就迎刃而解了。