高中向量教学中数学思想的渗透

高中向量教学中数学思想的渗透

梁林

东莞市虎门外语学校

摘 要：随着教学改革的不断深化，我国教学事业迎来了全新的挑战。数学是高中教学体系中的重要组成部分，这点自然也不例外。在高中数学教学中，向量教学占据的比重较大，有着一定的难度，学生在学习时难免会感到吃力、困难。为了帮助学生更好地掌握向量知识，广大教师积极革新教学思路，尝试运用数学思想实施教学。基于此，以下就将高中向量教学作为载体，着重分析数学思想的渗透路径，希望提供参考。

关键词：高中数学；向量教学；数学思想

向量是数学高考中的必考知识点，要想在此处不失分，就必须灵活掌握这部分知识，做到融会贯通。细心观察高中向量知识，可以发现其中蕴藏着深厚的数学思想，在教学过程中，如若教师可以巧妙地将数学思想渗透到向量教学当中，能够帮助学生更好地理解、消化向量知识。这样，学生在解答这类问题时，则能够得心应手、游刃有余。那么，在实际的高中数学向量教学中，可以从哪些方面入手，实现数学思想的有效渗透呢？具体如下。

一、数形结合思想的渗透

对于大部分学生而言，更多时候是运用数形结合思想实现“以形辅数”，以几何的方式思考、解答代数问题，彰显了图形的直观性、思维的辨识性和解答的简洁性。在高中数学向量教学中，教师同样也可以运用数形结合这一思想方法进行教学，在锻炼学生数学思维的同时，帮助学生更好地理解向量知识。例如：在向量教学中，常常会遇到这类问题，如下：“已知向量a≠e，|e|＝1，对任意t∈R，恒有|a－te|≥|a－1|，那么_.A.a⊥e。B.a⊥（a－e）。C.e⊥（a－e）。D.（a＋e）⊥（a－e）”，这是一道经典的高考题，体现了向量知识的魅力。其中，几何知识有些隐蔽，不易察觉，且难度不小，将参数融入向量知识，赋予其更多的可能。显然，一味地计算难以得出答案，此时教师则可以引导学生绘制出相应的图形，使数学问题图形化^[1]。在图形的辅助下，学生的思维得以启迪，明确该问题的本质，即点到直线距离的概念的内涵的几何属性，用向量的语言描述最小值，逐步求出问题的答案。显而易见，题目中描述的各种关系看似复杂，但是如果将其转变为直观的图形，那么就可以清楚地展示数量之间的关系，从而更快地得出结论，获得事半功倍之效。可见，在高中数学向量教学中运用数形结合思想是尤为重要且必要的。

二、数学建模思想的渗透

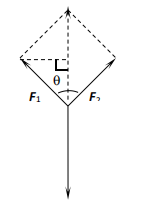
高中数学教学大纲和近几年的高考中愈加关注学生数学建模思想的培养和考察。在日常学习中，学生通过已有知识和经验构建数学模型，可以促进数学问题的解答，更加深刻、透彻地掌握数学知识，并实现知识的内化，将其转变为自己的能力^[2]。在高中数学课堂上，教师也可以将向量知识利用起来，有效锻炼学生的数学建模能力。例如：教师可以从学生的现实生活入手，引入一个熟悉的例子：“在生活中，可以发现这样的现象，即两个人共同提装有重物的袋子时，夹角越大，那么要用的力也更大；在引体向上运动中，两臂的夹角越大，耗费的力气也越大。同学们，站在数学的视角，我们应当如何解释这类现象呢？”对于这一问题，教师就可以用数学中的向量知识来表示力，将原本抽象的数学问题转变为数学模型，以便于问题的解答。如图一，可以设|F1|＝|F2|，根据课堂所学的向量的平行四边形法则、直角三角形以及力的平衡相关知识，可以得出这样的结论，即“|F1|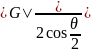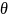＝ ”, 由0°到180°逐步增大时，那么 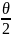由0°到90°逐步增大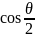， 的值则由大逐步缩小，所以|F1|由小逐步增大，换言之即F1和F2的夹角数值越大，那么就越费力，反之；则省力^[3]。不难看出，高中数学向量知识也和数学建模思想有着紧密的关联，所以在实际教学中，教师也可以通过数学建模思想实施向量教学，引领学生更加顺利地把握问题的本质，进而在解答问题时更加高效。

（图一）

三、分类讨论思想的渗透

在高中数学教学中，分类讨论思想是十分常见的，它是数学严谨性的有力体现，主要指的是一种在不同情形讨论研究对象的思想方法。同样的，在向量学习中，会遇到不少要用这一思想方法分析、解答的，因此分类讨论思想在高中数学向量教学中的渗透也十分关键^[4]。例如：就“Rt△ABC中，AB＝（2，3），AC＝（1，k），请问实数k多少？”这一问题来说，认真审题，可以发现问题并没有清楚地指出该三角形的直角是哪个角，因此针对这一问题的解答，就要对直角的位置进行分类讨论，即∠A＝90°、∠B＝90°或者∠C＝90°这三种情况。可以看出，将分类讨论思想渗透到高中数学向量教学中，能够促进学生对数学问题的理解和把握，培养学生理清数学问题本质和规律的能力，助推学生数学综合素质的发展。

四、方程思想的渗透

除了数形结合思想、数学模型思想以及分类讨论思想以外，方程思想也是向量问题解答中的关键，值得受到充分的重视。例如：有这样一道题目：“向量a、b满足|a|＝|b|＝a·b＝2，且（a－c）·（b－2c）＝0，请问|b－c|的最小值为？”可以明确的一点是，向量a和b满足夹角为60°，且模长都是定值，这个问题也可以通过坐标化的代数运算进行解答。在高中数学向量教学中，对于这类较为特殊的问题，就可以通过方程思想，将模长问题转变为方程运算，让运算过程变得跟更加简单、便捷。

结束语：

总而言之，数学思想在高中数学向量教学中的渗透，能够深化学生对向量知识的理解，优化学生的数学知识框架，对于学生数学学习的深入大有裨益。高中数学教师是教学活动的组织者和开展者，更是学生学习、成长道路中的引路人，更要充分认识到数学思想的价值和优势，积极寻找数学思想和向量知识之间的契合点，并且通过行之有效的方法加以融合，努力为学生构建更加优质的学习环境，让学生从中积累丰富知识和技能，为后续学习创造良好前提。

参考文献：

[1]顾道德. 如何用数学思想解平面向量题[J]. 语数外学习, 2019, (005):34-34.

[2]陈蓥. 运用数学思想,提升解平面向量题的效率[J]. 语数外学习：语文教育, 2019,(006):40-40.

[3]刘佳, 李琪, 苏淑华,等. 新课标下高中数学教材例题设置的难度研究——以平面向量为例[J]. 科教导刊, 2019(20):2-2.

[4]魏琦. 高中数学向量解题基本思想与技巧分析[J]. 数学学习与研究:教研版, 2020(7):139-139.