浙江省富阳中学
摘要 :函数与导数中的零点问题是近几年全国高考的热点。由于这类问题具有知识点多,方法灵活,综合性强等特点,学生很难掌控。本文尝试通过梳理解决函数与导数中的零点问题的六个常见基本对策,帮助学生形成解决这类问题的解题程序和相应知识网络,促进学生原有零散知识的结构化沉淀。
关键词:零点问题 常用对策
函数与导数中的零点问题是近几年全国高考热点、难点问题。由于以函数与导数中的零点问题为代表的多变量问题并不是某一章节或知识模块内容,而是贯穿高中数学各个知识模块之间,学生在这方面的知识容易碎片化,因此这类问题也一直是学生的痛点问题。纵观近年全国高考数学试题,函数双(多)零点问题题干设计呈现出两大特征:第一类直接描述函数的零点(比如2016高考全国卷1第21题;2018年高考新课标1卷理科第21题;2022高考全国甲卷理科第21题;2022高考全国乙卷理科第21题);第二类间接描述函数的零点(比如2018年高考全国1卷第21题;2021高考全国1卷第22题;2022高考全国1卷第22题)。 可见,在近几年的全国高考的函数与导数解答题中,命题教师不回避这一热点,几乎年年考查。由于处理这类问题的方法难度较大,难以表述,很多老师在高考复习教学中感到不知所措。为了更精准地备考,这里笔者总结了几种解决这类问题的基本策略。
例1若函数![]() 存在两个不同零点
存在两个不同零点![]() 且
且![]() .求证:
.求证:
(1)![]() (2)
(2)![]() (3)
(3)![]()
策略1 消元法
(1)分析:对于双元问题,我们一般的处理方法是引导学生通过消元变为单元.由题知![]() ,可得
,可得![]() ,当且仅当
,当且仅当![]() 取得。
取得。
策略2 换元法(比值代换)
(2)分析:对于双元![]() ,
,![]() 难以自身消元时,通过变形获得不涉及字母
难以自身消元时,通过变形获得不涉及字母![]() 的
的![]() ,
,![]() 的关系
的关系
式,关系式可以改变为![]() ,对过比值换元,令
,对过比值换元,令![]() ,则
,则![]() ,可知
,可知![]() ,从而
,从而![]() ,
,![]() ,即证:
,即证:![]()
![]() ,即证:
,即证:![]() ,令
,令![]() ,可知
,可知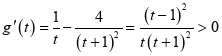 ,可知
,可知![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,故
,故![]() ,得证.
,得证.
策略3 对称化构造函数法
(3)分析:如果把本问题看作函数极值点偏移问题。由![]() 两个零点可知关于
两个零点可知关于![]() 的方程
的方程![]() 有两个正根,令
有两个正根,令![]() ,可知
,可知![]() 为极值点,且
为极值点,且![]() ,故即证
,故即证![]() ,而
,而![]() 在
在![]() 上单增,即证
上单增,即证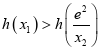 ,即证
,即证 ,令
,令 ,可知
,可知![]() ,即
,即![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,故
,故![]() ,得证.
,得证.
策略4 对数平均不等式法
分析:对于(3),我们也可以先利用对数平均不等式:![]() 来消元。将关系式
来消元。将关系式![]() 变形为
变形为![]() ,即证:
,即证:
 ,即证:
,即证: ,令
,令![]() ,即证:
,即证:![]() 。
。
事实上,上述推理告诉我们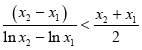 ,其中
,其中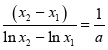 ,故得证.
,故得证.
评析:消元思想是处理双变量问题的核心策略。通过比值换元、整体换元也可以实现减元的目标。对数平均不等式的本质即齐次化下的比值换元,而比值换元比对数平均不等式具有更广泛的适用性。
例2 已知函数![]() 有两个零点
有两个零点![]() 且
且![]() .求证:
.求证:![]() 且
且![]() .
.
策略5 同构法
分析:通过恒等式![]() 可以有效沟通指对数,帮助化简该函数,易知
可以有效沟通指对数,帮助化简该函数,易知![]() ,从而令
,从而令![]() ,可得到复合函数
,可得到复合函数 ,易知
,易知![]() ,
,![]() ,此时
,此时![]() 有唯一正根
有唯一正根![]() ,由
,由![]() 可知由两个交点
可知由两个交点![]() ,易知当
,易知当![]() 时,
时,![]() ,
,![]() ,即
,即![]() 也是
也是![]() 的零点,同理
的零点,同理![]() 也是
也是![]() 的零点,即方程
的零点,即方程![]() 和
和![]() 同根,从而
同根,从而![]() ,由对数平均不等式可知
,由对数平均不等式可知 ,得证.
,得证.
例3 已知![]() ,求证:
,求证:![]() .
.
策略6 放缩法
分析:令函数![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() 分别有两交点
分别有两交点![]() ,
,
 由熟知不等式:
由熟知不等式:![]()
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
所以![]() ,由
,由![]() 单调性知
单调性知![]() ,
,
![]() ,由
,由![]() 单调性知
单调性知![]() ,
,
 如右图.而
如右图.而![]() 与
与![]() 有两交点
有两交点![]() 时满足:
时满足:![]() 为
为![]() 两根,即
两根,即![]() ,从而
,从而![]() ;
;
再令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,可知
,可知![]() ,当
,当![]() 时,
时,
令![]() ,
,
![]() ,可知
,可知![]() 在
在![]() 上递增,且
上递增,且![]() ,故
,故![]() ,从而当
,从而当![]() 与
与![]() 有两交点
有两交点![]() ,与
,与![]() 和
和![]() 分别交于
分别交于![]() ,类似可知
,类似可知![]() ,
,![]() ,从而
,从而![]() ,而
,而![]() ,故
,故![]() .
.
事实上,上述问题的目标还可以进行如下的变式:
变式1:利用常见函数不等式![]() ,我们能否探
,我们能否探
究出一个关于![]() 的新结论?
的新结论?
提示:![]() ,结论为:
,结论为:![]()

变式2:如果采用两条切线放缩,能否得到新的结论?
提示:易知![]() .
.
变式3:如果采用两条割线放缩,能否得到新的结论?
 提示:易知
提示:易知![]() .
.

说明:其实本题令![]() ,即有
,即有![]() ,则可证
,则可证![]() .
.
变式:已知函数![]() ,设
,设![]() 为两个不相等的正数,且
为两个不相等的正数,且![]() ,求证:
,求证:![]()
分析:由题知![]() ,即
,即![]() ,令
,令![]() ,即当
,即当![]() 时,证明:
时,证明:![]() .令
.令![]() ,
,![]() ,即回到例3.
,即回到例3.
评析:合理地改变函数形式或者条件结构有助于解题。从解题中容易发现,比值换元在本题十分有效,对数平均不等式在本题不能直接使用。对数平均不等式的本质即齐次化下的比值换元,而比值换元比对数平均不等式具有更广泛的适用性。同时通过换元方法,可以改变条件结构构造新的问题,也是一种良好的命题思路。