构建函数模型比大小

构建函数模型比大小

李倩

汉中中学

本篇文章将通过具体例题的解析，由浅入深的呈现出如何通过构造函数解决不等关系的比较，不等式的证明这类题目进行解决。

1.比较的大小。

解析：设函数，因为，所以函数在第一象限单调递增，，所以

分析：观察已知条件，发现指数相同，可以把看成幂函数值。

启发：比较大小的两个数值，若底数相同，构建指数函数；若指数相同，构建幂函数；同类思想，可以构建所学的基本函数解决相关问题。

2.若，，，则（）

A.a

解析：因为， ， ，所以选A。

分析：这道题的难点在于大小的比较，由于任意角的三角函数定义是通过单位圆刻画的，所以我们可以建立单位圆模型，将数值的大小有形化为线段与弧长长短的比较。具体过程如下：

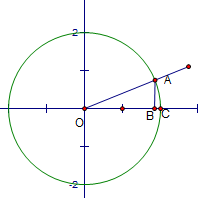
由任意角正弦值的定义可得 ，

由弧长的计算公式可得。因为，即

所以，。

启发：对于非特殊角三角函数值，我们可以通过建立单位圆模型，使得三角函数值以正弦线，余弦线，正切线线段,弧长具像呈现出来，借助线段，弧长长短的比较解决非特殊角三角函数值大小的比较的问题。

3. 已知为定义在R上的可导函数，为其导函数，且 恒成立，其中e 是自然对数的底数，则（  ）

解析：答案 B

设函数则，由，可得，所以，所以单调递增，则，即

。

分析：这道题的难点在于由已知条件，借助构建。结合考虑所要解决的问题：大小，可转化为大小的比较，与所构建函数形式统一，从而解决问题。

启发：这是一道导数型构建函数模型，对于这类题目的解决，我们要把握已知条件中含导数的不等式，其实它等价于含导数式子的正负性，我们结合所要解决的问题外在形式，构建函数模型，使得对其求导后，能由已知条件的正负得到构建函数的导函数的正负，从而得到函数的单调性，利用函数单调性解决大小比较的问题。

4. 已知 且，则（    ）

解析：答案 B

因为所以。

设，则。

设  ，则

所以在上单调递减。当时，所以即故在上单调递减。因为，所以。

分析：可以先对已知条件进行整理，将含的式子分置于等式两边，通过形式的同构，将原式转化为不等关系，从而构造出函数模型，将不等关系转化为函数值的大小，即可通过研究函数单调性得到自变量之间的大小关系。

本题有两个难点：

①利用对数的运算性质，将原式进行整理，使得含a,b的式子分别位于等式两边；

②用同构函数的思想，对原式进行适当放缩，将题目转化为已知函数值大小，从而利用函数单调性，得到自变量之间的大小比较。

启发：建立同构函数思想，对所求解问题外在形式进行适当的变形（等价变形，适当放缩），使得外在结构一致，即可构建出函数。

5.已知函数f(x)＝aln x＋x.

(1)讨论f(x)的单调性；    (2)当a＝1时，证明：.

解析：f(x)的定义域为(0，＋∞)，  f′(x)＝＋1＝.

当a≥0时，f′(x)>0，所以f(x)在(0，＋∞)上是增加的．

当a<0时，若x∈(－a，＋∞)，则f′(x)>0；

若x∈(0，－a)，则f′(x)<0.  所以f(x)在(－a，＋∞)上是增加的， 在(0，－a)上是减少的．

综上所述，当a≥0时，f(x)在(0，＋∞)上是增加的；当a<0时，f(x)在(－a，＋∞)上是增加的，在(0，－a)上是减少的．

(2)证明　当a＝1时，要证 ，即证，即证.

令函数g(x)＝1＋，则.

令g′(x)>0，得x∈(0，e)；令g′(x)<0，得x∈(e，＋∞)．

所以g(x)在(0，e)上是增加的，在(e，＋∞)上是减少的，所以g(x)max＝g(e)＝1＋，

令函数，则.当x∈(0,2)时，h′(x)<0；

当x∈(2，＋∞)时，h′(x)>0.所以h(x)在(0,2)上是减少的，在(2，＋∞)上是增加的，

所以.因为，所以h(x)min>g(x)max，

即，从而得证．

分析：在第二问的解答中，将不等式转化为两个函数的最值进行比较，指数对数分置不等号两边，由，证明成立。

本题需要突破两个难点：

①指对分离，熟悉超越函数模型。

②成立是的必要不充分条件。

启发：建立指对分离，异构函数的数学思想方法。建立不同函数模型，用最值之间的关系，达到对不等式的证明。

我们通过几个例题展示了从不同角度构造出函数模型，利用函数的单调性，最值来解决比大小，不等式证明相关问题。在同构函数问题上，都有一个共同方向，通过观察，变形，放缩等方法，寻求外在形式的统一性，抽象出对应的函数模型。在异构函数方法的应用中，往往可以指对分离，对基本初等函数及超越函数熟悉的前提下，将分离的函数进行适当的变形，使其最值可以求解出来，通过各自最值的比较达到不等式关系的证明。用这种方法证明不等式，需再次强调，成立是的必要不充分条件。