高等数学中基本概念的可视化与思政教学设计初探——以定积分为例

高等数学中基本概念的可视化与思政教学设计初探——以定积分为例

张海波

武警工程大学基础部高等数学教研室  陕西西安

摘要：一个国家只有数学蓬勃的发展，才能展现它国力的强大。数学的发展和至善和国家繁荣昌盛密切相关。诚如数学家柯西所言，“一个国家的科学水平可以用它消耗的数学来度量”。而高等数学是大学的一门重要课程，数学概念是其最基本的构筑单位，对数学概念的理解程度直接影响着学生对该课程的学习和掌握。以高等数学最为核心的概念之一定积分为例，本文基于学生已有的数学基础，通过数形结合的数学思想及问题驱动的教学方法，最终引出该新概念的定义。并探究其在其他方面的相关应用及利用定义的计算方法，同时在引入环节、正文环节及应用拓展环节均结合具体内容，恰当融入相应思政元素，合理进行思政设计。

关键词：高等数学；定积分；数形结合；问题驱动；课程思政

引言

十七世纪中叶，在欧洲，封建制度逐渐灭亡，资本主义正值发展，生产力得到了解放，工业和科学技术得到了前所未有的大发展，比如采矿冶炼、机器制造、天文观测、远洋航海、枪炮制造等。生产实践给科学研究带来了一系列新的课题，对这些课题做进一步研究又给数学提出了了一个又一个的新问题，这些问题归纳起来有四类，对这四类问题科学家们都进行了探讨，得到了可喜的结果，尤其是英国的物理学家、数学家牛顿，他从变速直线运动的瞬时速度出发进行了深入的研究。德国的数学家、物理学家莱布尼兹从曲线的切线问题入手进行了深入的研究，他们分别独立的创造了微积分，因此被称为微积分的创始者。

在这四类问题中，对前三类问题的探讨建立了微分学的概念；对第四类问题的探讨，我们将建立另外一个新的概念“定积分”。

思政设计：微积分数学史引入，融入课程思政元素。

一、问题背景

  1.情景再现

每年夏天，受极端降雨影响，洪涝地质灾害频发；作为武警部队职能使命之一，每当危难来临，武警官兵总能冲锋在前、勇挑重担，持续奋战在防汛与抗洪一线，用忠诚担当守护万家灯火，以实际行动守卫人民群众生命财产安全，彰显了人民子弟兵的初心和本色。

思政设计：以武警部队职能任务，对水域面积丈量进行引入；即吸引学员注意力也突出实战化导向。

那么，防汛或抗洪期间，如何有效的组织、科学的分配人力物力，从而有针对性的进行高效驰援呢？这里一个简单的考虑：就是根据防汛湖泊或受灾淹没区域的面积来确定相关力量配备！

进一步，防汛湖泊或受灾淹没区域的面积又如何确定呢？

如图所示，是某片防汛湖泊或受灾淹没区域的模拟现场；为求其面积，先描绘出边界轮廓！求这个防汛湖泊或受灾淹没区域的面积也就是求对应的平面图形的面积！

对于平面图形的面积求解问题，如果是中学：

我们已经学习过矩形、三角形、平行四边形、梯形、多边形这样的一些由直线构成的规则图形的面积求解方法，其中矩形最简单，其他则可以通过分割的方式转化成矩形，然后求出面积！

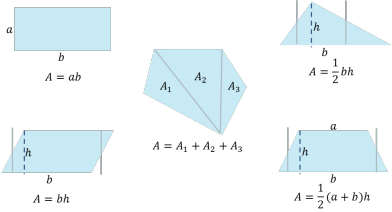
而对于由曲线构成的不规则图形的面积求解比如圆，仍然是通过分割方式进行，但对于必然存在的曲线则考虑以直代曲的近似处理方式，转化为已知的、能够求解面积的规则图形来近似计算不规则图形的面积，这也是微积分思想的核心之一；并通过不断的分割最终转化为求解矩形的面积！

人类认识事物的一般规律是从已知的知识出发去探知新的知识。大家会想到，用两组相互垂直的平行直线簇将湖面进行分割。我们发现中间部分都是规则的矩形，它们的面积就是长乘宽，而边缘部分不规则的图形的面积如何得到呢？

我们一起分析一下这种图形的特点：它有三条直线边，其中有一条直线边垂直于另外两条直线边，第四条是曲线边，数学上把这种图形叫做曲边梯形。

2.曲边梯形的面积：（如何计算呢？）

(1).定性分析——第一层次

[以直代曲]

由于它是含有一条曲边的不规则图形，要求其面积，根据已有方法显然只能当作规则图形进行近似求解，即以直代曲！那么，当成什么样的规则图形？基于曲边梯形的特点（两条平行线加一条垂直线）考虑用最简单的矩形近似即可；具体地，我们以曲边梯形底边x∈[a,b]为矩形长、对应曲线y=f(x)上任取一点作为矩形宽（考虑为了更方便地观察我们取左端点）所得矩形面积作为曲边梯形面积的一个近似！

[为了提高近似的精度减少近似的误差，分割以直代曲再求和]

但是由于整条曲线高度起伏变化幅度太大，只以曲边梯形整个底边x∈[a,b]为矩形长、在整条曲线上任取一点为矩形宽作一个矩形来代表曲边梯形，显然其代表性并不理想，得到的面积误差一般也会很大；可以想见如动图所示，对曲边梯形的底边x∈[a,b]分割的越多便可得到越窄的小曲边梯形对应作矩形近似，各矩形与各小曲边梯形的吻合程度越高，用这些矩形的总面积对整个曲边梯形面积进行近似，面积误差也就越来越小，几乎肉眼无法分辨。

(2).定量分析——第二层次

我们将前面的过程给以准确的数学描述，步骤可以归结为：

(1)分割

在区间内插入个分点，并让，，于是将区间分成 个小区间，过每个分点作垂直于

轴的直线，就将曲边梯形分割成个小的曲边梯形，，这一过程称为“化整为零”。

现在只要对小的曲边梯形作一计算就行了。如何做呢？

(2)以直代曲

在上用直线段代替曲线段，即“以直代曲”。

以直代曲的思想在生活、工程、科学研究中处处都有，比如这个烟囱的远视图，它是个圆台体，而事实上，它是由一块块砖头砌成的。砖头的边缘都是直线段，而砌成的烟囱却是一个圆台体，因此恩格斯深刻地指示“高等数学的主要基础之一是这样一个矛盾；在一定条件下，直线和曲线是一回事”。在什么样的条件下呢？（停顿）就是在无限细分，在局部的小范围内，直线和曲线是一回事。

(3)求和

将每个小曲边梯形作同样的处理，加起来，就得到了大曲边梯形面积的“近似值”，这一过程叫做“积零为整”。

我们遇到了“精确”与“近似”的矛盾，从以前的分析我们知道“无限细分将会导致无限接近”，这就是极限的思想。

(4)取极限

令，则

一定存在，这就是曲边梯形的面积，我们称这一过程为“取得精确”，这个让的过程就体现了“无限细分，无限接近”。

实际上，在工业、农业、工程等领域中的很多问题都可以归纳为这样一种结构。因此，数学作为人类活动量性表达的学科就有必要给这一结构进行研究和讨论，这就是本节的主要内容“定积分”。

二、定积分的概念

1.定义：设函数在上有界，在中任意插入个分点

把区间分成个小区间，各小区间的长度依次，，在各小区间上任取一点（），作乘积并作和，记，如果不论对怎样的分法，也不论在小区间上点怎样的取法，只要当时，和总趋于确定的极限，我们称这个极限为函数在区间上的定积分，记为

2.在定积分的定义中，我们要注意以下几点：

(1).“一个不同”

在学习过程中，许多学员可能认为“”和“”是一回事，实际不然，（画图说明）在均分的情况下，“”和“”是等价的，但定义的要求是任意分割，任意取值。

(2).“两个相关”

定积分的数值只与被积函数和积分区间有关。

(3).“三个无关”

当函数在上可积时，定积分值从定义我们看到：两个任意，一个不同的极限过程才能确定积分的存在性，使得和式的计算非常复杂。哪些函数满足这样的条件呢？

3.数学思想与哲学内涵

分割   → 化整为零（局部对整体的否定）

取近似 → 以直代曲（量变）

求和   → 积零为整（整体对局部的否定）

取极限 → 取得精确（量变产生质变的规律）

(1).化整为零是对整体的否定、积零为整是对局部的否定，两次否定诚如恩格斯在《反杜林论》中指出：在求无穷小量总和的极限中，否定之否定表现的尤为突出！

(2).一次次的取近似是量变的积累，而利用取极限取得精确则是质的突破，量质互变归率得以体现！

(3).局部与整体、近似与精确之间的矛盾关系，充分体现了哲学上的对立统一观点！

思政设计：利用动态的课件展示如何求解曲边梯形的面积，通过重点演示直与曲的转化、有限与无限的转化，启发学生领悟知识点背后蕴含的辩证唯物主义的哲学思想。

三、拓展应用

1.不规则图形的面积

(1).定积分思想的萌芽

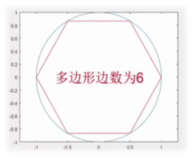
(2).方法发展：

·为什么面前的定积分却是“西方进口”的？

·为什么萌芽在东方，发展却在西方？

·“分割”+“求和”， 还缺少了什么？

思政设计：以微积分方法思想启蒙在东方、应用发展在西方的事实，即让学员感受民族文化所取得辉煌成就的自豪感，又引发学员对民族文化遗憾落寞的思考。

2.其他领域

对于非均匀变化的量在有限区间上求总量问题，都可以通过定积分来解决，即

例  某军事防御工程现对其挖掘的隧道进行评估，通过对隧道区域横截面积的分析，可以辅助评估人员进行评价，试求隧道的横截面的面积。

分析：通过建模与编程实现

% 定积分的近似计算(矩形法)

syms x

f = -3/8 x^2+6;

a = -4;

b = 4;

% 划分的子区间数

n = 150;

dx = (b - a) / n;

x = a:dx:b;

approx_s = dx * sum(y);

disp(['定积分的近似计算结果(矩形法):', num2str(approx_s)]);

approx_s=31.9675

参考文献

[1]同济大学数学科学学院. 高等数学[M]. 北京:高等教育出版社. 2023