从人口模型的研究例说数学建模的模型求解

从人口模型的研究例说数学建模的模型求解

曾翰举

福建省三明第一中学 福建三明 353000

摘要：参数拟合可以在不同阶段以不同方法进行，拟合效果有差别。拟合效果可以用残差图来观察，但是预测效果必须用新的数据来观察，不能用“用于拟合的数据集”来检验“预测效果”。对于关键参数，有时需要人为给定一个先验值，但是严谨起见需要观察这个先验值的波动对结果的影响是否明显，最好选取一个效果最优的值。非线性拟合相较线性拟合不仅更难计算，而且对于数据的波动反应更为敏感。线性化是一个非常有效的方式，但是二者的结果并不能完全等价，只是两种近似方法。观察误差大小时，应结合绝对误差和相对误差综合观察。

关键词：人口模型；数学建模；模型求解

在研究了人口模型的基本假设，符号约定，模型建立，以及模型求解后，我们的求解还停留在符号和理论层面，我们如果需要确定参数，就需要基于历史数据。

下面这张表格，是我国大陆地区常住人口数的数据，它的数据来源有三个，分别是：户籍统计数、年度人口普查数据、非普查年度的年度人口抽样调查的推算数据。

有了数据表以后，我们完全可以以年份 为横坐标，以人口数 为纵坐标，来画出数据的散点图，如图6.1

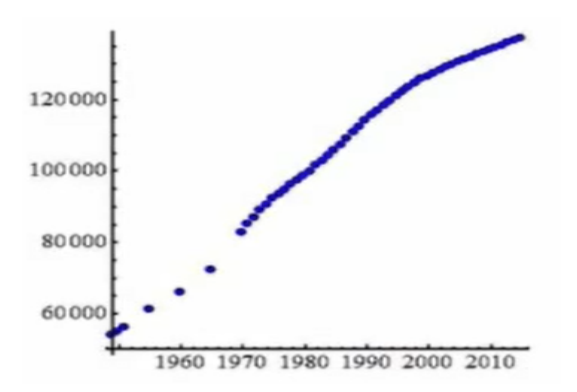
(图6.1)

画出散点图后我们很容易看出一个趋势，即一开始先快速增加，然后缓慢增加。当然如果我们这个散点图的比例尺画的不太好，我们可能就看不出来这种趋势，例如将纵轴比例尺压得足够扁，那么整幅散点图看上去像是一个线性趋势，这其实是一个误区。我们要调整，看能够以什么样的比例尺，能够更好的反映数据的趋势。

1．参数拟合：离散模型拟合

首先拟合人口模型在离散形式下的参数，形式为 ，它是一个数列的递推关系式，由前一项确定后一项，参数是 和 。面对这个递推关系式我们表格中的前面几组数据是没有办法使用的，因为这个递推关系是由前一项推后一项，但在表格的前几年当中并非年年都有数据，这是由自然条件，还有社会环境所决定，所以这几年的数据我们没有办法使用。从1970到2015年间这样的数据是每年都有，所以我们用1970到2015年间的数据拟合我们的参数 和 。

我们先做一个代数变形，把 除到左边去，之所以要除，是因为我们希望左边的式子 与右边 成一个线性关系，即： 。

它确定了一个线性关系，这个线性关系的一次项系数是 ，常数项是 。我们通过对①式进行最小二乘的线性拟合，可以求出 和 的值，进而能求出 和 。

，

因为 的单位是万人，这意味着我们通过这种方式能够得到一个人口上限的预测值，即人口上限 为15亿4333万人。我们看拟合效果的好坏，即下个图6.2，当中的蓝色的点是真实数据，黄色的点是从1970年作为数列的首项，利用我们关系式推算出来的数据。

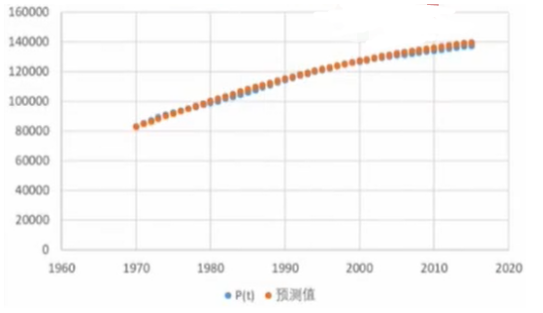
(图6.2)

我们可以看到实际数据离我们递推关系推算出来的数据很接近，说明拟合的效果还是不错的。

如果我们以1970年为首项，进行计算，一直推算到2016年的人口数，得到 为14亿人，这距离国家统计局发布的正式数据13亿8271万的相对误差只有1.51%。

但是如果我们直接利用我们最小二乘法拟合得到的关系式：

直接代入2015年的真实数据，去预测2016年的人口数据，我们得到的预测值为13亿8000万人，距离2016年实际数据13亿8271万人误差仅为0.082%，就是小数点后4位的误差，所以实际上我们利用离散模型的递推关系，从哪里开始推算，对于我们的预测效果其实是差别是很大的。

2．参数拟合：连续模型拟合(1)

我们也可以拟合连续模型当中的参数， 这是我们的连续模型，其中参数是 和 ，是两个正待定常数。数据是 ， ，其横坐标是第 个年份，纵坐标是对应的人口数的真实值， 是总共有多少个数据。我们试图用 ， 这些数据来拟合 中的参数 和 。

首先我们做一个代数变形， 除到左边去，

再做一个近似处理，

这里的近似原理是用平均变化率来逼近瞬时变化率，即 ，在这样的变形下，如果把左边 当成一个整体，然后把右边的 也当成一个整体，二者之间就是一个线性的关系，线性关系就可以使用最小二乘法的线性组合去找到 的值和 的值，进而求出 和 的值。

那为了要对 这个式子进行线性回归，拟合为一次函数关系 ，我们需要将一开始的数据进行变换，变换的方式如下：

令 ， ，则有：

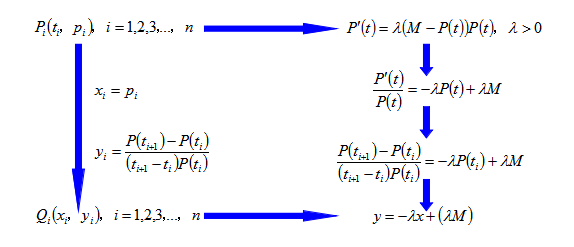
即：现在的 是我们 这个式子的观察值，现在的 是我们 这个式子的观察值，我们试图用数据点 去拟合连续模型当中的参数 和 ，现在变成用数据点 用最小二乘法线性拟合一个线性函数。

拟合的结果为 ， ， 的单位为万人，此时我们的 用连续模型拟合出来人口极限数量实际是16亿2128万人，这和离散模型当中的结果是有差异的，预示着我们使用不同的拟合方式，对连续模型的拟合，对离散模型的拟合，所预测出来的极限人口数其实是不一样的。

3．参数拟合：连续模型拟合(2)

当然，我们对连续模型 进行参数拟合，所用的方法并不是唯一的。我们知道，使用微分方程求 的解析解为 。我们可以直接用数据 对这个非线性函数进行最小二乘法的拟合，由于拟合过程是非线性的，所以需要解的是一个非线性方程组。

这里直接给出拟合结果 万人，这意味着这种方式预测到的人口数量极限约为10亿8111万人。这个解肯定与我们现实是不符的，因为我们目前的人口数就已经比这个数据多了。

但如果去掉前10个数据进行拟合得到的结果，就会变大一些，此时 ；去掉前20个数据会更大，得到 ；去掉前30个数据时 ；去掉前40个数据，得到 ，去掉前50个数据， 。我们看到 的拟合值在逐渐增大，越来越接近于真实的情况。

这意味着什么呢？这意味着如果我们直接对非线性的目标函数进行最小二乘拟合的话，受数据波动的影响就比较大。因为我们都知道1970年前后的数据，对现在的指导意义远没有2010年以后的数据对现在的指导意义大，所以我们去掉前面的数据，只用后面的数据进行迎合，效果就会越来越好。所以如果数据是以时间序列的方式进行呈现的，那么较早的数据就会造成拟合效果的失真，这种失真会随着非线性的增加而增加，也就是我们平时说的混沌效应。

4．参数拟合：连续模型拟合(3)

我们当然还可以将非线性方程转化为线性方程，用线性化的方法来拟合 的参数。

我们还是一样对 的非线性代数式作一个代数变形，在我们推导 的解析式的时候得到 ，在这个代数式当中将左侧 当作一个整体 ，右边 当作一个整体 ，那么就会出现一个线性关系式 ，我们通过最小二乘法线性拟合来确定 还有 的值。

我们首先做一个变换， ， ，现在的 是 的观察值，现在的 是代数式 左边的观测值，通过 ，我们用最小二乘法进行线性拟合就可以确定 还有 的值。

但此时需要先知道 的值才能得到 ，也才能够得到 这个数据点，有了 我们才能够做最小二乘法，再进行线性拟合来得到 的值。即我们要得到 的值，得先有 ，但要把 变成 我们得先知道 的值，这里面出现了一个循环论证式的矛盾。

那这个矛盾怎么去解决呢？其实我们可以先人为的确定 大概的值，然后用最小二乘法去拟合，拟合之后再看一看效果。

当然这里面我们不能只指定一个 值，我们要指定多个不同的 值，去看它们的效果对比，如果出现 值在一定范围内变化，对拟合效果影响不大，那这种方法就是比较合理的，我们可以确定一个 的大概的值，就可以得到一个比较可靠的拟合效果。但是假如 的微小波动会带来拟合效果的巨大变化，那么我们这种方式就不可以，因为我们人为确定 大概的值总会有一个偏差，如果这个模型相对于 这个参数来说，变化是非常敏感的，那么我们人为设定的 值所带来的偏差就会引起拟合效果的巨大偏差，那这个时候这种方法就是不能采用。

我们分别取 等于14亿，15亿，16亿和17亿，来看拟合的效果对比和残差图(如图6.3)，其中蓝色的点是真实的数据点，红色的点用相应的 值进行拟合计算出来的参数带入到 这个函数当中后，所得到的 的函数图像。

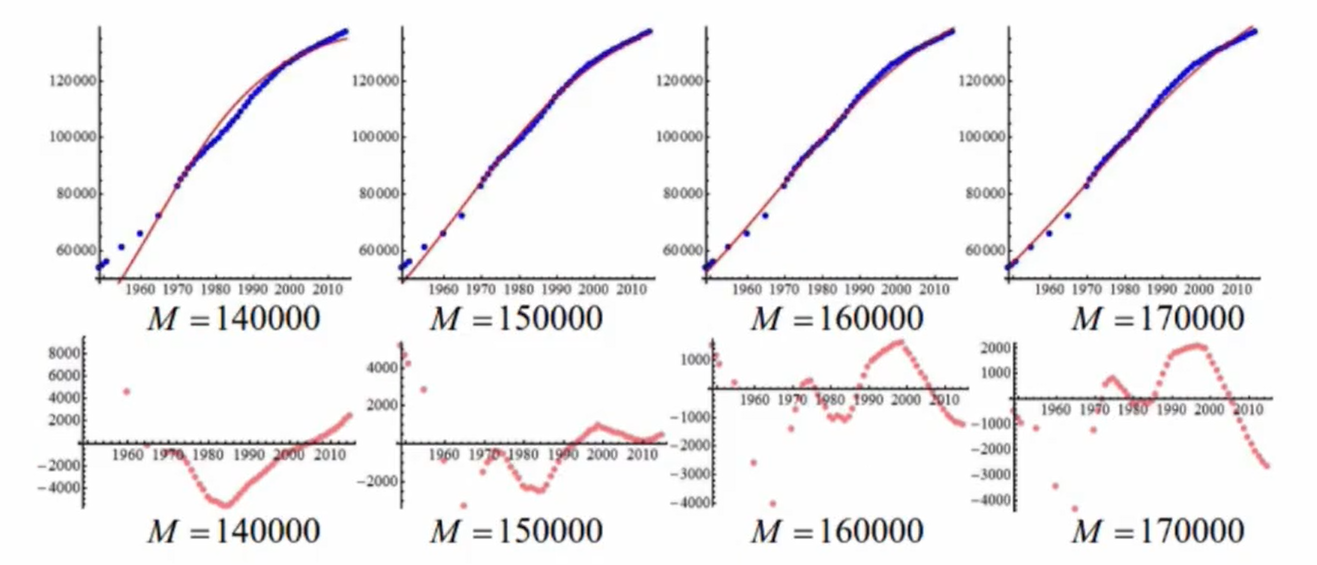
(图6.3)

我们可以看到，当 在15亿，16亿和17亿这个范围内变化的是时候，它的残差图的变化并不是特别的明显，基本上都是正负 万~ 万这个范围，所以我们认为这个模型对于 这个参数来说比较稳健，即我们只要取一个大一点的 的值，就可以得到一个比较好的拟合效果。并且当我们对比一下残差图，还是能比较哪个 值是相对来说拟合的更好一些。

实际上从残差图可以看得出来，当 为16亿的时候，它的拟合效果会相对来说更好一些。相应的 的解析式为这样一个函数：

当我们把2016带进去，我们去预测2016年的人口数，得到的数值，就是13亿9408万人，国家统计局发布的真实数据13亿8271万人，相对误差是 。

不仅如此，如果我们仔细的去观察这个残差图，其实我们可以看出很多事情，比如说什么时候是出国热，什么时候是回国热，什么时候是自然灾害，哪几年有社会运动，包括计划生育的影响等等，其实都可以通过残差图看出来，因为残差图是真实值和拟合值之间的差距，拟合值预示着这一年应该是多少，但真实值就反映真实的情况。所以真实情况与拟合的情况会有偏差，那这个偏差的原因是什么呢？就有可能是各种各样的社会事件。

5．总结

参数拟合可以在不同阶段以不同方式进行，拟合效果会有差别。比方说我们可以在解出解析解之前，针对方程来进行参数拟合，也可以再解出解析解之后，针对函数进行参数拟合。我们可以针对连续函数模型进行参数拟合，可以针对离散模型。我们可以对非线性函数进行参数拟合，也可以线性化以后再进行参数拟合，都是可以的。但是计算的路径，还有拟合效果会有差别，需要各位同学仔细体会。

考察拟合效果好与不好的时候，我们可以用残差图来观察，但是我们来考察预测效果好与不好，我们就不能够用“用于拟合”的数据来检验，因为如果你模型拟合的还不错的话，你的拟合效果肯定是可以的，你拿拟合效果来预测效果，这是不合理的。所以加入我们是用1949~2015年的数据来进行拟合，那我们用来检验预测效果就要用2016年的数据来检验。

对于关键的参数，有的时候需要人为的指定一个先验值，但是严谨起见，需要观察这个先验值的波动对结果的影响是不是明显，当然最好选取一个效果比较优的一个检验值，是最好的。

非线性拟合较线性拟合不仅更难以计算，而且对于数据的波动反应更为敏感，线性化是一个非常有效的方式。但是二者的结果并不完全等价，这只是两种近似的方法，

再有就是观察误差大小的时候，我们应该结合绝对误差和相对误差综合来观察，不能够只观察绝对误差，当然也不能够只观察相对误差。

参考文献：

[1]李虎.中学数学建模案例分析——以人口模型为例.福建中学数学,2020(4)：43-46.

[2]王勇.Logistic人口模型的求解问题.哈尔滨商业大学学报(自然科学版),2006,(5).58-59.

[3]任运平,杨建雅.LOGISTIC人口模型的改进[J].河东学刊,1999,(6).23-24.

注：三明市基础教育科学研究2020年度(专项)课题立项《数学建模在高中数学课堂教学中的实践研究》立项编号：JYKT-20003研究成果(3)

7/7