广东省湛江市二中海东中学 524000
摘要:函数最值问题一直是高中数学教学中的一个重点内容,近几年高考模拟题、高考题频繁出现。本文主要探讨开区间内连续函数(含参数)最值的问题,利用导数这一工具来判断函数的单调性,对函数在极值点处的函数值和在开区间端点处的函数值进行比较,从而确定最值取得的情况,最后解决参数的取值范围。
关键词:连续函数;开区间;单调性;最值;参数
在数学分析中,函数的最值问题是一个经典且重要的问题。由最值定理可知,对于闭区间上的连续函数,函数一定有最大值和最小值。然而,当函数定义域换成开区间时,函数是否存在最值就需要具体分析了。本文将对开区间内连续函数的最值问题进行详细地探讨和研究,并给出解决与最值有关参数取值范围的策略。
引理:如果在闭区间![]() 上,函数
上,函数![]() 的图像是一条连续不断的曲线,那么它一定有最大值和最小值.
的图像是一条连续不断的曲线,那么它一定有最大值和最小值.
问题:如果把闭区间![]() 换成开区间
换成开区间![]() ,连续函数
,连续函数![]() 是否一定有最值呢? 下面进行详细的分类讨论。
是否一定有最值呢? 下面进行详细的分类讨论。
一、开区间内连续函数最值问题分类讨论
对于开区间内连续函数,其最值情况可以分为以下几种类型:
1. 函数在开区间内单调
如果连续函数![]() 在开区间
在开区间![]() 内单调,则函数
内单调,则函数![]() 在该区间内既没有最大值,也没有最小值。
在该区间内既没有最大值,也没有最小值。
2. 函数在开区间内只有一个极值点的情况

 如果连续函数
如果连续函数![]() 在开区间
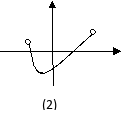
在开区间![]() 只有一个极值点,结合函数的单调性,可知这个极大(小)值点也是函数
只有一个极值点,结合函数的单调性,可知这个极大(小)值点也是函数![]() 最大(小)值点。如下图(1)、(2)所示:
最大(小)值点。如下图(1)、(2)所示:
3. 函数在开区间内有两个极值点的情况
如果连续函数![]() 在开区间
在开区间![]() 内有两个极值点,函数的最值情况需要分类讨论,此时函数
内有两个极值点,函数的最值情况需要分类讨论,此时函数![]() 图像可能有以下几种情况,如下图所示:
图像可能有以下几种情况,如下图所示:

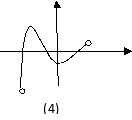


如上图(3)中,函数既无最大值,也无最小值;图(4)中,函数只有最大值,没有最小值;图(5)中,函数只有最小值,没有最大值;图(6)中,函数既有最大值,也有最小值。
4、函数在开区间内有多个极值点的情况
如果函数![]() 在开区间
在开区间![]() 内有多个极值点时,需要比较所有极值与端点函数值的大小,最大的一个值(非端点值)即为函数最大值,否则函数没有最大值;同理,最小的一个值(非端点值)即为函数最小值,否则函数也没有最小值。
内有多个极值点时,需要比较所有极值与端点函数值的大小,最大的一个值(非端点值)即为函数最大值,否则函数没有最大值;同理,最小的一个值(非端点值)即为函数最小值,否则函数也没有最小值。
二、开区间内连续函数最值问题解决策略
对于开区间内连续函数的最值问题,我们可以采用以下策略进行求解:
1. 求函数的导数
函数的导数是通过求函数在某一点的变化率来反映函数的单调性和极值点。因此,当我们要解决一个函数的最值问题时,通常需要求出该函数的导数。通过分析导数的正负和零点,可以帮助我们快速确定函数在某一区间内的单调性和极值点的位置,因此求函数的导数是解决最值问题的第一步。
2. 分析函数的单调性
通过导数,我们可以分析函数在开区间![]() 内的单调性。如果导数
内的单调性。如果导数![]() ,函数在该区间内单调递增;如果导数
,函数在该区间内单调递增;如果导数![]() ,则函数在该区间内单调递减,此时,函数在该区间内既没有最大值,也没有最小值。
,则函数在该区间内单调递减,此时,函数在该区间内既没有最大值,也没有最小值。
3. 确定函数的极值点
如果函数在开区间![]() 内不单调,即在该区间内既有递增又有递减,则需要确定函数的极值点。函数的极值点可以通过求导并令导数等于零来确定,导函数的零点就可能是极值点,当然需要进一步判断该点左右两侧导数是否异号,通过这种方法,我们可以准确地确定函数在开区间
内不单调,即在该区间内既有递增又有递减,则需要确定函数的极值点。函数的极值点可以通过求导并令导数等于零来确定,导函数的零点就可能是极值点,当然需要进一步判断该点左右两侧导数是否异号,通过这种方法,我们可以准确地确定函数在开区间![]() 内的极值点。
内的极值点。
4. 比较函数值
比较函数在极值点处的函数值和函数在开区间![]() 端点处的函数值,可以确定函数的最值。
端点处的函数值,可以确定函数的最值。
5. 确定参数的取值范围
根据函数最值的情况,建立符合条件的不等式关系,当然参数的取值范围需要满足函数最值的要求,最后确定参数的取值范围。
三、开区间内连续函数最值问题实例讲解
例题:若函数![]() 在
在![]() 有最小值,则
有最小值,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
分析:这是一个典型的开区间内连续函数最值问题,故我们可以用导数来研究此函数问题,首先对此函数![]() 进行求导,分析函数的极值与端点函数值,从而解决最值相关问题。因为
进行求导,分析函数的极值与端点函数值,从而解决最值相关问题。因为![]() ,令
,令![]() ,则
,则![]() 或
或![]() .显然
.显然![]() ,因为若
,因为若![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 单调递增,此时没有最小值,故不符合题意。所以
单调递增,此时没有最小值,故不符合题意。所以![]() 有两个不同的极值点,
有两个不同的极值点,![]() 和
和![]() .
.
由于![]() ,下面对
,下面对![]() 的取值范围进行分类讨论:
的取值范围进行分类讨论:
(I)若![]() 时,导函数
时,导函数![]() 的图像大致如图(7)所示:
的图像大致如图(7)所示:

可以发现:当![]() 时,
时,![]() ;当
;当![]() ,
,![]() .所以
.所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,故
单调递增,故![]() 在
在![]() 内只有极小值
内只有极小值![]() ,此时极小值也是函数的最小值.此时
,此时极小值也是函数的最小值.此时![]() 符合题意.
符合题意.
(II)若![]() 且
且![]() ,具体对
,具体对![]() 的取值分为两部分:
的取值分为两部分:![]() 和
和![]() .
.
 (i)如果
(i)如果![]() ,导函数
,导函数![]() 的图像大致如图(8)所示:
的图像大致如图(8)所示:
![]()
可以发现:当![]() 时,
时,![]() ;
;![]() ,
,![]() ;当
;当![]() 时
时![]() .所以
.所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增. 故
单调递增. 故![]() 在
在![]() 处取得极小值
处取得极小值![]() .又
.又![]() ,函数
,函数![]() 在
在![]() 内是否存在最小值,需要比较端点处函数值
内是否存在最小值,需要比较端点处函数值![]() 和极小值
和极小值![]() 的大小,只有当
的大小,只有当![]() ,即
,即![]() 时,函数
时,函数![]() 有最小值
有最小值![]() .此时
.此时![]() 符合题意.
符合题意.
 (ii)如果
(ii)如果![]() ,导函数
,导函数![]() 的图像大致如图(9)所示:
的图像大致如图(9)所示:
由图可知:当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ;当
;当![]() 时,
时,![]() .
.
 所以
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增.此时
单调递增.此时![]() 在
在![]() 处取得极小值
处取得极小值![]() .又
.又![]() ,函数
,函数![]() 在
在![]() 内是否存在最小值,需要比较端点处函数值
内是否存在最小值,需要比较端点处函数值![]() 和极小值
和极小值![]() 的大小.因为当
的大小.因为当![]() ,端点值
,端点值
![]() ,而极小值
,而极小值![]() ,显然
,显然![]() ,此时函数
,此时函数![]() 没有最小值.所以
没有最小值.所以![]() 不符合题意.
不符合题意.
(III)若![]() ,导函数
,导函数![]() 的图像大致如图(10)所示:
的图像大致如图(10)所示:
由图可知:当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ;所以
;所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.此时函数
单调递减.此时函数![]() 在
在![]() 内没有最小值.所以
内没有最小值.所以![]() 不符合题意。综上(I)(II)(III)可知,若函数
不符合题意。综上(I)(II)(III)可知,若函数![]() 在
在![]() 有最小值,则
有最小值,则![]() .
.
结语:通过对开区间内连续函数最值问题的分类讨论和解题策略的介绍,我们可以发现,解决这类问题需要综合运用导数、单调性、函数值比较等知识。在实际求解过程中,需要根据函数的具体情况进行分析,灵活运用各种方法,才能找到最值并确定参数的取值范围。
参考文献:
[1]黄明秋.开区间内连续函数最值问题的探讨[J].湖北农机化 2020(02):172-173.
[2]覃运初.开区间上的连续函数[J].安庆师范学院学报(自然科学版)2003(11):43-44.